|
|
备注:知乎专栏更新了数理化生四科的基础讲义,更加完善的第二版已经更新,并且附上可以直接下载打印的PDF文档,里面可能还有一些小的笔误,订正后会再更新。
数学基础讲义大合集:数学基础讲义完整合集下载(含目录)
数学解题思路大合集:数学解题思路完整合集下载(含目录)
化学讲义合集:化学基础讲义合集
化学解题小合集:化学解题思路合集下载-2020年北京山东江苏浙江全国一二三
心得体会小合集:学习心得体会2021合集下载
物理和生物若急用可以先看知乎专栏里的,PDF文档待更新完善后再放出
下面是正文:
空间向量在高中数学主要是解题的工具,基本概念的内容很少,与平面向量相似。
建议多用纸和笔来实际模拟,以及自己画空间直角坐标系来观察。
<hr/>一、 空间直角坐标系
类似平面直角坐标系,我们可以建立空间直角坐标系,如下图所示。

在空间里,除了x轴、y轴,还有z轴,经过原点,与平面xOy垂直。
就好比把现实中的地图上,除了标记地址方位外,还要标记高度,比如某楼层的高度。
在空间里,每个点有3个坐标:x轴坐标,y轴坐标,z轴坐标,类比地图上就是经度(东西)、纬度(南北),高度(上下),记作(x,y,z)
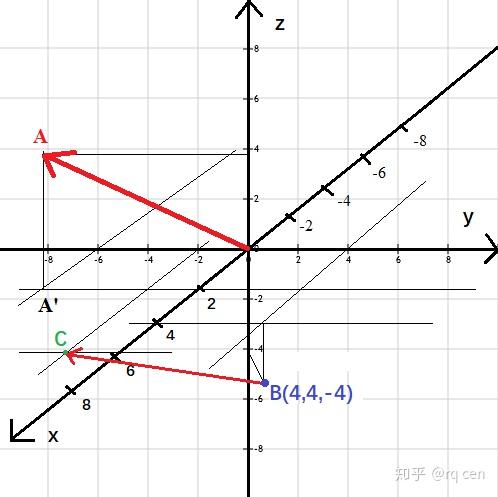
比如点A(2,-6,4),它的x轴坐标是2,y轴坐标是-6,z轴坐标是4

从点A直接向x轴、y轴、z轴引垂线,交点分别为(2,0,0)(0.-6,0)和(0,0,4)
也可以先从点A向平面xOy引垂线,交于点A&#39;,再从A&#39;向x轴和y轴引垂线,结果是一样的,看起来更加直观。
空间里两点A (x_{a},y_{a},z_{a}) 和B (x_{b},y_{b},z_{b})之间的距离为: \sqrt{(x_{a}-x_{b})^{2}+(y_{a}-y_{b})^{2}+(z_{a}-z_{b})^{2}}
<hr/>二、空间向量
与平面向量类似,空间向量也包含了“方向”和“量”两层含义。不同之处在于这是在三维空间里。
任何空间向量也都可以用三维坐标(x,y,z)来表示,表示分表在x轴、y轴、z轴方向移动的距离。
沿用上面的例子,不过不是点A(2,-6,4),而是向量OA(2,-6,4)(OA上面应该有个箭头,由于输入法的原因无法实现)

它代表沿x轴方向移动+2个单位,沿y轴方向移动-6个单位,沿z轴方向移动4个单位
这个移动的方式与起点在哪里无关,向量是可以任意平移的
假设起点位置在B(4,4,-4),那么终点位置C的坐标就是:
(4+2,4-6,-4+4),也就是(6,-2,0)
空间向量的运算与性质与平面向量极其类似
2.1 相加
对于空间向量a (x_{a},y_{a},z_{a}) 和空间向量b (x_{b},y_{b},z_{b})
它们的和a+b为 (x_{a}+x_{b},y_{a}+y_{b},z_{a}+z_{b})
2.2 平行
如果空间向量a与b平行,则存在非零常数 \lambda 使得: x_{a}=\lambda x_{b} ,y_{a}=\lambda y_{b} ,z_{a}=\lambda z_{b}
反之也成立。
2.3 内积(点乘)
空间向量a (x_{a},y_{a},z_{a}) 和空间向量b (x_{b},y_{b},z_{b})的内积(点乘)为:
a· b=x_{a}*x_{b}+y_{a}*y_{b}+z_{a}*z_{b}
2.4 垂直
如果空间向量a (x_{a},y_{a},z_{a}) 与空间向量b (x_{b},y_{b},z_{b})垂直,则有
a· b=x_{a}*x_{b}+y_{a}*y_{b}+z_{a}*z_{b}=0
反之也成立
2.5 夹角
空间向量a (x_{a},y_{a},z_{a}) 与空间向量b (x_{b},y_{b},z_{b})的夹角为:
cos\theta=(a·b)/(|a|*|b|)=(x_{a}*x_{b}+y_{a}*y_{b}+z_{a}*z_{b})/(\sqrt{x_{a}^{2}+y_{a}^{2}+z_{a}^{2}}\sqrt{x_{b}^{2}+y_{b}^{2}+z_{b}^{2}})
2.6 空间直线的方向向量
对空间内任意直线,无论把它如何平移,它的方向都是不变的。
这很容易理解,本身向量就像是有长度、有方向的线段,可以任意平移,这个向量的方向,就是它所在的直线的方向
要求直线的方向向量,只需要从直线上任取两点,把它们的坐标相减即可,与平面坐标中类似。
2.7 空间直线的法向量?
平面直线有法向量,求法同学们应该掌握了,那么空间直线呢?
事实上,过空间直线上一点,与它垂直的向量有无穷多,形成了一个平面
比如空间直角坐标系上的z轴,过原点与z轴垂直的向量无穷多,只要是xOy平面上的直线都与z轴垂直
2.8 平面的法向量
虽然空间直线没法确定一个法向量,但是空间平面可以!
只要是与该平面垂直的向量就是它的法向量。
用上面的例子,坐标系中xOy平面的法向量就是z轴,或者任意的向量(0,0,z)(z≠0)都是它的法向量
2.9 几个基础命题
下面3个基础命题摘自课本
基础命题1:两条直线平行或重合的充要条件是他们的方向向量互相平行。
这个很容易理解,不解释。
基础命题2:一条直线与一个平面平行或在一个平面内的充要条件是这条直线的方向向量垂直于该直线的法向量
用1支笔代表直线,一张纸代表平面,再用一支笔代表该平面的法向量,比划一下即可知。
基础命题3:两个平面平行或重合的充要条件是它们的法向量相互平行。
用2支笔和2张纸比划下即可知。
根据以上命题易得:两个平面垂直的充要条件是它们的法向量垂直。
<hr/>三、空间向量的应用
空间向量较多应用在证明和求距离、夹角的题目中,以棱柱,特别是正方体、长方体中最多
比如下例
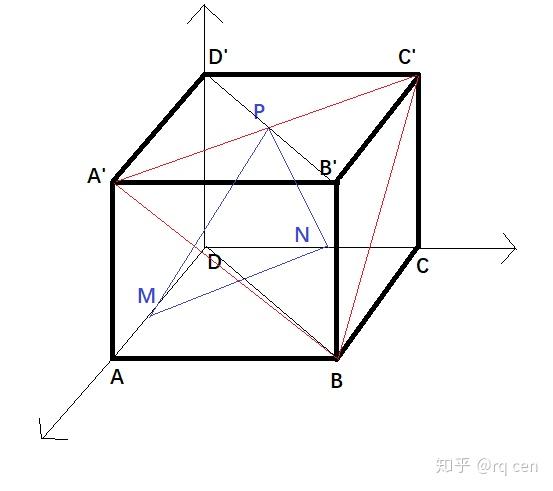
正方体ABCD-A&#39;B&#39;C&#39;D&#39;中,M是AD的中点,N是DC的中点,P是A&#39;C&#39;的中点
那么平面MPN与平面A&#39;BC&#39;的夹角是什么呢?
下面提供一种思路:
因为M、N分别为AD和DC的中点,所以MN∥AC
又因为ABCD-A&#39;B&#39;C&#39;D&#39;是正方体,所以AC∥A&#39;C&#39;
所以MN∥A&#39;C&#39;
又因为P在A&#39;C&#39;上,所以MNPA&#39;C&#39;共面
所以A&#39;C&#39;就是平面MPN与平面A&#39;BC&#39;的交线
下面只要在这两个平面内分别找A&#39;C&#39;的垂线就可以了。
对于平面MPN:易证MNC&#39;A&#39;是等腰梯形,因此MN的中点(设为Q)与P的连线就与A&#39;C&#39;垂直
对于平面A&#39;BC&#39;:易证△A&#39;BC&#39;是等腰三角形,因此BP垂直于A&#39;C&#39;
只要找到BP与PQ的夹角就可以了
现在以D为原点(0,0,0),DA为x轴正方向,DC为y轴正方向,DD&#39;为z轴正方向,正方体边长为1,建立空间直角坐标系
则B(1,1,0),P(1/2,1/2,1),Q(1/4,1/4,0)
向量BP=(-1/2,-1/2,1),向量PQ=(-1/4,-1/4,-1)
用公式可以求得:
|cos\theta|=|BP·PQ|/(|BP||PQ|)=\sqrt{3}/3
因此二面角为 arccos(\sqrt{3}/3)
<hr/>小结
空间向量在高中并不是重点考察的内容,是非常好用的工具,通常需要配合空间几何的定理一起使用。
空间向量的关键还是找关系,通过平行线找二面的交线、通过平移直线让两条直线共面、通过做垂线找到点到面的距离。
空间向量最有用的是可以直接代入坐标数值进行计算,对证明垂直、求角度、距离是非常有用的。
如果平面向量非常熟练的话,空间向量掌握起来会更加容易。 |
|