|
|
一、基本概念及性质
1.定义
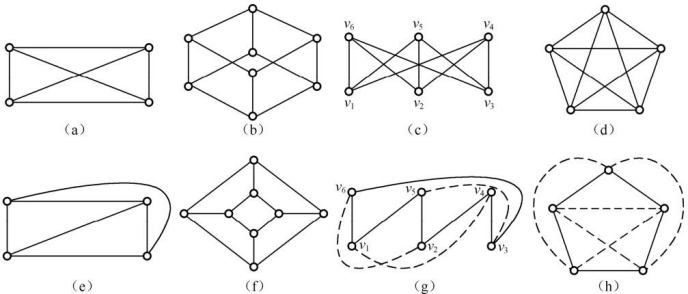
在一个平面上,如果能够画出无向图 G 的图解,其中没有任何边的交叉,则称图 G 是个平面图;否则,称 G 是非平面图。
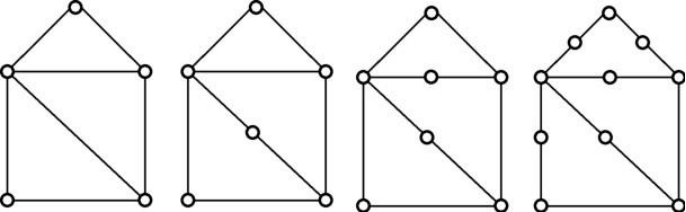
有些图从表面上看,它的某些边是相交的,但是不能就此肯定它不是平面图。
对于图(a)(b)中的无向图来说,加以重画之后,它将不包含任何边的交叉(e)(f)。(a)(b)是平面图,而(c)(d)是非平面图。
2.观察法
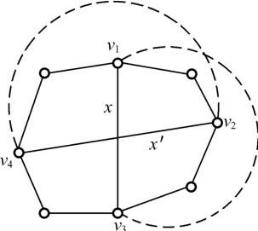
设 C=v_1v_2v_3v_4v_1 是图 G 中的任何基本回路, x=v_1v_3 和 x '=v_2v_4 是图 G 中的任意两条基本路径。若 x 和 x ' 同时在 C 的同一侧,则两者必定发生交叉。
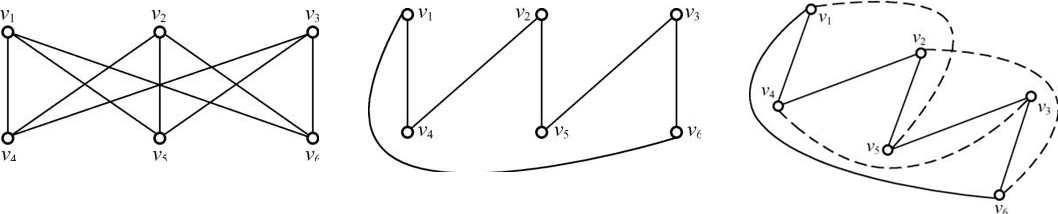
观察法可判断 K_{3,3} 不是平面图。给定 K_{3,3} 中有一个基本回路 C= v_1 v_6 v_3 v_5 v_2 v_4 v_1 ,考察三条边 \left\{ {v_1,v_5 } \right\} , \left\{ {v_2,v_6 } \right\} , \left\{ {v_3 ,v_4 } \right\} ,显然,三条边中至少有两条边同时处于 C 的同一侧,因此避免不了交叉。
3.库拉托夫斯基定理
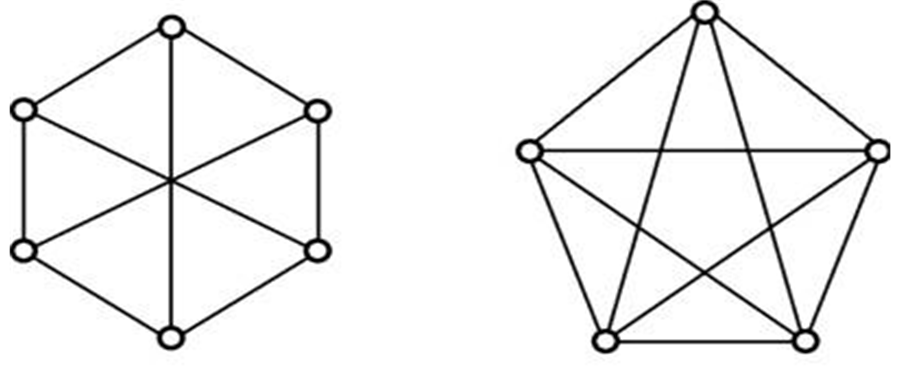
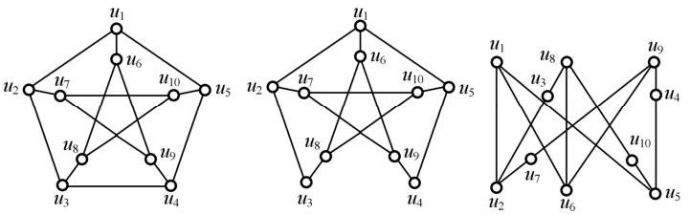
库拉托夫斯基图:由观察法均可证明, K_{3,3} 与 K_5 都是非平面图, K_{3,3} 是边最少的非平面图, K_5 是结点最少的非平面图。
同胚操作:在原图的边上增加或者删除度数为 2 的结点,不会影响图的平面性。

同胚图:设 G_1 和 G_2 是两个无向图。如果 G_1 和 G_2 是同构的,或者通过同胚操作,能够把 G_1 和 G_2 转化成同构的图,则称 G_1 和 G_2 是同胚的。
库拉托夫斯基定理:设 G 是一个无向图。图 G 中不存在任何与 K_{3,3} 或 K_5 同胚的子图,当且仅当图 G 是平面图。
应用库拉托夫斯基定理,通过同胚操作,可证明下图均为非平面图。
二、多边形的图
1.多边形的图的归纳定义
① 单个基本回路的图,称为多边形。一个多边形是一个多边形的图。
② 设 G=\left<V,E,ψ\right> 是一个多边形的图;另设 P=(v_iu_1u_2…u_{l-1}v_j),(l≥1 ) 是任意基本路径,不与图 G 中任一路径交叉,且有 v_i,v_j∈V , u_k ∉V 。
于是,由图 G 和 P 所构成的图 G&#39;=\left<V&#39;,E&#39;,ψ&#39;\right> 也是一个多边形的图,其中
V&#39;=V\cup\left\{ u_1,u_2,\dots,u_{l-1} \right\}
E&#39;=E\cup\left\{ \left\{ u_i,u_1 \right\},\left\{ u_1,u_2 \right\},\dots,\left\{ u_{l-1},v_j \right\} \right\}
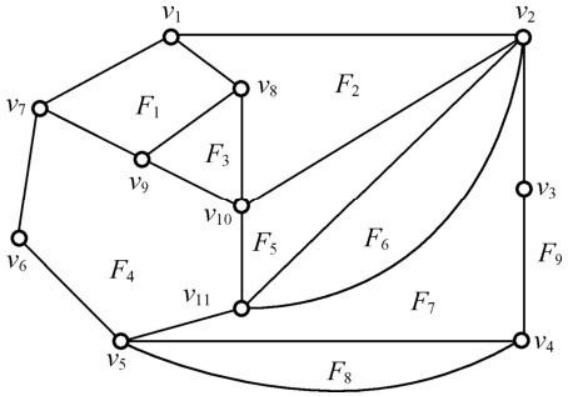
多边形的图
2.多边形图的面
多边形图中的多边形能够把平面划分成数个区域,每一个区域都称为图 G 的面。
如果两个面共有一条边,则称这样的两个面是邻接的面。
如上图中的区域 F_1,F_2,\dots,F_9 是面, F_1,F_2就是邻接的面。
3.极大基本回路
包含有多边形的图 G 的所有面的边界的多边形,称为 G 的极大基本回路。
图中 (v_1v_2v_3v_4v_5v_6v_7v_1) ,就是该多边形的图的极大基本回路。
如果图 G 在平面上,其极大基本回路外侧的无限区域,称为 G 的无限面。
如果图 G 在球面上,则 G 的无限面等同其它的有限面。
4.欧拉公式
设 G=\left<V,E\right> 是个具有 k 个面(包括无限面)的多边形的图,则 \left| V \right| − \left| E \right| + k = 2
证明:对于面的数目 k,用归纳法证明
① 面的最少数目(包括无限面)是 k = 2 。在这种情况下,图 G 是个多边形,因而应有 \left| V \right|=\left| E \right|。这样,有 \left| V \right| − \left| E \right| + k = 2 。
② 假设对于具有 k-1 个面(包括无限面)的图来说,定理成立。
要证对于具有 k 个面(包括无限面)的图,定理亦成立。首先构造具有 k&#39;= k-1 个面的的图 G&#39;=\left<V&#39;,E&#39;\right> ,然后附加上一条长度为 l≥1 的基本路径,它与 G&#39; 恰有共有两个结点,则 \left| V \right|-\left| E \right|+k=(\left| V&#39; \right|+l-1)-(\left| E&#39; \right|+l)+(k′+1)=\left| V&#39; \right|-\left| E&#39; \right|+k&#39;
根据归纳假设可知, \left| V&#39; \right|-\left| E&#39; \right|+k&#39;=2
三、对偶图
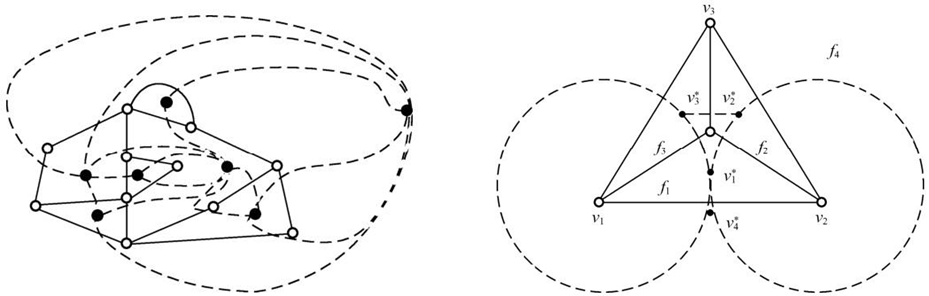
设多边形的图 G=\left<V,E\right> ,其含有面 F_1 ,F_2,\dots,F_n ,包括有无限面,则可用一下方法构造 G 的对偶图 G^* :
在 F_i 内画出每个 F_i 对应的结点 v^*_i ,并且连通 v^*_i 和 v^*_j ,去交叉 F_i 和 F_j 所有公共的边。易知 G 和 G^* 是互为对偶的。
如果 G 与 G^* 同构,则称 G 是自对偶图。
推论:若平面图 G=\left<V,E\right> 是自对偶图,则 2\left| V \right|-\left| E \right|=2 。
证明:由于图 G 是自对偶图,则有 \left| V \right|=k ,由欧拉公式易证。
四、着色问题
对于地图的着色问题,可以化为其对偶图的结点的着色问题。
着色:对图 G 的每个结点指派一种颜色,使得相邻结点都有不同的颜色。
若可用 n 种颜色对图 G 着色,则称 G 是n-可着色的, n 的最小值记为 \chi (G) 。
四色定理:任何简单平面图都是 4-可着色的。
五色定理:任何简单平面图 G=\left<V ,E\right> ,均有\chi(G)\leq5。 |
|