|
|
在阅读LIO-SAM源码的时候,发现点线残差和点面残差和雅克比构建采用了LOAM的表示方法。由于采用了欧拉角构建旋转矩阵,使得雅克比推导和优化方程构建比较复杂,代码也比较难阅读。A-LOAM中使用四元数表示旋转,使用了ceres自动求导,省去了雅可比的推导过程,代码大大简化。LIO-SAM作为一项非常优秀的3D激光SLAM框架,在进行当前帧点云位姿优化的时候使用了Eigen库构造优化过程,后续加入GPS和回环因子又用了gtsam因子图优化,作为对比,gtsam的代码封装性极强,作者把两种优化方式融合到了一个框架中,达到了很好的效果,因此有必要对代码中对应的公式进行推导。
scan2MapOptimization()
点线面残差和雅克比构建主要的代码在LIO-SAM/src/mapOptmization.cpp的scan2MapOptimization()函数中,流程如下:
// 进行角点和平面匹配并构建残差
cornerOptimization();
surfOptimization();
// 将两中特征点匹配的残差组合
combineOptimizationCoeffs();
// 对残差进行一次优化,如果收敛则提前结束
if (LMOptimization(iterCount) == true)
break;
点线残差构建
点线残差的定义为点到线的距离,在该直线上取两个点 A=(x1,y1,z1), B=(x2,y2,z2),设当前点为 P=(x0,y0,z0),如下
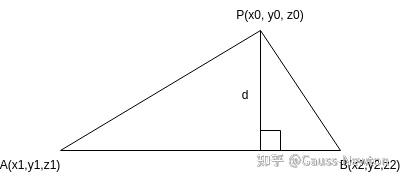
计算 △PAB的面积,除以AB即可,即
\mathrm{d}=\frac{|\mathbf{PA} \times \mathbf{PB}|}{|\mathbf{AB}|}
\begin{aligned} S_{\triangle A B P} \propto|\overrightarrow{P A} \times \overrightarrow{P B}| \\ \overrightarrow{P A} \times \overrightarrow{P B}=&\left|\begin{array}{ccc} i & j & k \\ x_{1}-x_{0} & y_{1}-y_{0} & z_{1}-z_{0} \\ x_{2}-x_{0} & y_{2}-y_{0} & z_{2}-z_{0} \end{array}\right| \\ =& {\left[\begin{array}{c} \left(y_{1}-y_{0}\right)\left(z_{2}-z_{0}\right)-\left(z_{1}-z_{0}\right)\left(y_{2}-y_{0}\right) \\ \left(z_{1}-z_{0}\right)\left(x_{2}-x_{0}\right)-\left(x_{1}-x_{0}\right)\left(z_{2}-z_{0}\right) \\ \left(x_{1}-x_{0}\right)\left(y_{2}-y_{0}\right)-\left(y_{1}-y_{0}\right)\left(x_{2}-x_{0}\right) \end{array}\right] } \\ \overrightarrow{P A} \times \overrightarrow{P B} \mid &=(\overrightarrow{P A} \times \overrightarrow{P B})^{T}(\overrightarrow{P A} \times \overrightarrow{P B}) \\ &=\left(\left(y_{1}-y_{0}\right)\left(z_{2}-z_{0}\right)-\left(z_{1}-z_{0}\right)\left(y_{2}-y_{0}\right)\right)^{2} \\ &+\left(\left(z_{1}-z_{0}\right)\left(x_{2}-x_{0}\right)-\left(x_{1}-x_{0}\right)\left(z_{2}-z_{0}\right)\right)^{2} \\ &+\left(\left(x_{1}-x_{0}\right)\left(y_{2}-y_{0}\right)-\left(y_{1}-y_{0}\right)\left(x_{2}-x_{0}\right)\right)^{2} \end{aligned}
对应代码中
// 计算 PA x PB 的模长
float a012 = sqrt(((x0 - x1)*(y0 - y2) - (x0 - x2)*(y0 - y1)) * ((x0 - x1)*(y0 - y2) - (x0 - x2)*(y0 - y1))
+ ((x0 - x1)*(z0 - z2) - (x0 - x2)*(z0 - z1)) * ((x0 - x1)*(z0 - z2) - (x0 - x2)*(z0 - z1))
+ ((y0 - y1)*(z0 - z2) - (y0 - y2)*(z0 - z1)) * ((y0 - y1)*(z0 - z2) - (y0 - y2)*(z0 - z1)));
// 计算 AB 模长
float l12 = sqrt((x1 - x2)*(x1 - x2) + (y1 - y2)*(y1 - y2) + (z1 - z2)*(z1 - z2));
// P 到 AB 的距离
float ld2 = a012 / l12;
点线雅可比计算
分为两步,先对点求导,再对位姿求导
J=\frac{\partial d}{\partial T_{w b}}=\frac{\partial d}{\partial \boldsymbol{p}^{w}} \frac{\partial \boldsymbol{p}^{w}}{\partial \boldsymbol{T}_{w b}}
设 \boldsymbol{p}_{m}=\overrightarrow{P M}=\overrightarrow{P A} \times \overrightarrow{P B} ,残差为:
\begin{aligned} d \propto \sqrt{{ }\left(\left(y_{1}-y_{0}\right)\left(z_{2}-z_{0}\right)-\left(z_{1}-z_{0}\right)\left(y_{2}-y_{0}\right)\right)^{2} \\ +\left(\left(z_{1}-z_{0}\right)\left(x_{2}-x_{0}\right)-\left(x_{1}-x_{0}\right)\left(z_{2}-z_{0}\right)\right)^{2} \\ +\left(\left(x_{1}-x_{0}\right)\left(y_{2}-y_{0}\right)-\left(y_{1}-y_{0}\right)\left(x_{2}-x_{0}\right)\right)^{2}} \\ = \sqrt{\boldsymbol{p}_{m}^{T} \boldsymbol{p}_{m}} \\ = \sqrt{\left(p_{m x}^{2}+p_{m y}^{2}+p_{m z}^{2}\right)} \end{aligned}
分别对(x0,y0,z0)求导
\begin{aligned} \frac{\partial d}{\partial \boldsymbol{p}^{w}} &=\left[\begin{array}{c} \frac{\partial d}{\partial x_{0}} \\ \frac{\partial d}{\partial y_{0}} \\ \frac{\partial d}{\partial z_{0}} \end{array}\right]^{T} \\ & \propto \frac{1}{2}\left[\begin{array}{c} 2 p_{m y}\left(\left(z_{2}-z_{0}\right)-\left(z_{1}-z_{0}\right)\right)+2 p_{m z}\left(\left(y_{1}-y_{0}\right)-\left(y_{2}-y_{0}\right)\right) \\ 2 p_{m z}\left(\left(x_{2}-x_{0}\right)-\left(x_{1}-x_{0}\right)\right)+2 p_{m x}\left(\left(z_{1}-z_{0}\right)-\left(z_{2}-z_{0}\right)\right) \\ 2 p_{m x}\left(\left(y_{2}-y_{0}\right)-\left(y_{1}-y_{0}\right)\right)+2 p_{m y}\left(\left(x_{1}-x_{0}\right)-\left(x_{2}-x_{0}\right)\right) \end{array}\right]^{T} \\ &=\left[\begin{array}{l} p_{m y}\left(z_{2}-z_{1}\right)+p_{m z}\left(y_{1}-y_{2}\right) \\ p_{m z}\left(x_{2}-x_{1}\right)+p_{m x}\left(z_{1}-z_{2}\right) \\ p_{m x}\left(y_{2}-y_{1}\right)+p_{m y}\left(x_{1}-x_{2}\right) \end{array}\right]^{T} \end{aligned}
对应代码中,代码中对向量|AB||PM|除是为了进行单位化
// 计算残差对点 P 的雅可比且进行单位化
float la = ((y1 - y2)*((x0 - x1)*(y0 - y2) - (x0 - x2)*(y0 - y1))
+ (z1 - z2)*((x0 - x1)*(z0 - z2) - (x0 - x2)*(z0 - z1))) / a012 / l12;
float lb = -((x1 - x2)*((x0 - x1)*(y0 - y2) - (x0 - x2)*(y0 - y1))
- (z1 - z2)*((y0 - y1)*(z0 - z2) - (y0 - y2)*(z0 - z1))) / a012 / l12;
float lc = -((x1 - x2)*((x0 - x1)*(z0 - z2) - (x0 - x2)*(z0 - z1))
+ (y1 - y2)*((y0 - y1)*(z0 - z2) - (y0 - y2)*(z0 - z1))) / a012 / l12;
点面残差计算
点到的平面的距离作为残差,对系数进行归一化处理,则计算方式为:
d_{h}=\frac{\left|pa \cdot x_{0}+ pb \cdot y_{0}+ pc \cdot z_{0}+pd\right|}{\sqrt{pa^{2}+pb^{2}+pc^{2}}}=\left|pa \cdot x_{0}+pb \cdot y_{0}+ pc \cdot z_{0}+pd\right|
对应代码为:
// 构建超定方程
for (int j = 0; j < 5; j++) {
matA0(j, 0) = laserCloudSurfFromMapDS->points[pointSearchInd[j]].x;
matA0(j, 1) = laserCloudSurfFromMapDS->points[pointSearchInd[j]].y;
matA0(j, 2) = laserCloudSurfFromMapDS->points[pointSearchInd[j]].z;
}
// 求解平面法向量,并单位化,单位化后的平面方程为 Ax + By + Cz + D = 0, A^2 + B^2 + C^2 = 1
matX0 = matA0.colPivHouseholderQr().solve(matB0);
float pa = matX0(0, 0);
float pb = matX0(1, 0);
float pc = matX0(2, 0);
float pd = 1;
float ps = sqrt(pa * pa + pb * pb + pc * pc);
pa /= ps; pb /= ps; pc /= ps; pd /= ps;
// 对每个点计算点到平面的距离,只有都在 0.2m 范围内才认为这个平面匹配是准的
bool planeValid = true;
for (int j = 0; j < 5; j++) {
if (fabs(pa * laserCloudSurfFromMapDS->points[pointSearchInd[j]].x +
pb * laserCloudSurfFromMapDS->points[pointSearchInd[j]].y +
pc * laserCloudSurfFromMapDS->points[pointSearchInd[j]].z + pd) > 0.2) {
planeValid = false;
break;
}
}
if (planeValid) {
// 用点到的平面的距离作为残差(带符号)
float pd2 = pa * pointSel.x + pb * pointSel.y + pc * pointSel.z + pd;
点面雅可比计算
用法向量作为雅可比,方向由 pd2 决定
// 用法向量作为雅可比,方向由 pd2 间接决定
coeff.x = s * pa;
coeff.y = s * pb;
coeff.z = s * pc;
coeff.intensity = s * pd2;
点线面残差对位姿的雅可比
\text { mat } A=\left[\begin{array}{c} \frac{\partial d}{\partial \text { roll }} \\ \frac{\partial d}{\partial p i t c h} \\ \frac{\partial d}{\partial y a w} \\ \frac{\partial d}{\partial t_{x}} \\ \frac{\partial d}{\partial t_{y}} \\ \frac{\partial d}{\partial t_{z}} \end{array}\right]
对平移的雅可比
雅可比推导分为两步,残差对点的雅可比和点对位姿的雅可比,下面推导点对位姿的雅可比
设 Lidar 相对于世界坐标系旋转矩阵为R ,平移为t ,将 Lidar 坐标系下的点转为世界坐标系的过程为:
\boldsymbol{p}^{w}=\boldsymbol{R} \boldsymbol{p}+\boldsymbol{t}
对平移的推导很简单,即
\frac{\partial \boldsymbol{p}^{w}}{\partial \boldsymbol{t}}=\frac{\partial \boldsymbol{R} \boldsymbol{p}+\boldsymbol{t}}{\partial \boldsymbol{t}}=\boldsymbol{I}
对应代码中
matA.at<float>(i, 3) = coeff.z;
matA.at<float>(i, 4) = coeff.x;
matA.at<float>(i, 5) = coeff.y;
对旋转的雅可比
LOAM 原作者选择的是 ZXY 外旋(沿固定 Z 轴旋转-> 沿固定 X 轴旋转 -> 沿固定 Y 轴旋转)表示,由于外旋的旋转矩阵顺序为作乘,因此 ZXY 内旋的旋转矩阵的计算方式为:R=RyRxRz,即:
\begin{aligned} \boldsymbol{R} &=\boldsymbol{R}_{y} \boldsymbol{R}_{x} \boldsymbol{R}_{z} \\ &=\left[\begin{array}{ccc} \cos (ry) & 0 & \sin (ry) \\ 0 & 1 & 0 \\ -\sin (ry) & 0 & \cos (ry) \end{array}\right]\left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos (rx) & -\sin (rx) \\ 0 & \sin (rx) & \cos (rx) \end{array}\right]\left[\begin{array}{ccc} \cos (rz) & -\sin (rz) & 0 \\ \sin (rz) & \cos (rz) & 0 \\ 0 & 0 & 1 \end{array}\right] \\ &=\left[\begin{array}{ccc} \cos (ry) \cos (rz)+\sin (ry) \sin (rx) \sin (rz) & \cos (rz) \sin (ry) \sin (rx)-\cos (ry) \sin (rz) & \cos (rx) \sin (ry) \\ \cos (rx) \sin (rz) & \cos (rx) \cos (rz) & -\sin (rx) \\ \cos (ry) \sin (rx) \sin (rz)-\cos (rz) \sin (ry) & \cos (ry) \cos (rz) \sin (rx)+\sin (ry) \sin (rz) & \cos (ry) \cos (rx) \end{array}\right] \end{aligned}
平移对旋转求导为0,忽略
点对rx求雅可比有:
\frac{\partial(\boldsymbol{R} \boldsymbol{p})}{\partial rx}=\left[\begin{array}{c} (\sin (ry) \cos (rx) \sin (rz)) p_{x}+(\cos (rz) \sin (ry) \cos (rx)) p_{y}-(\sin (rx) \sin (ry)) p_{z} \\ -(\sin (rx) \sin (rz)) p_{x}-(\sin (rx) \cos (rz)) p_{y}-(\cos (rx)) p_{z} \\ (\cos (ry) \cos (rx) \sin (rz)) p_{x}+(\cos (ry) \cos (rz) \cos (rx)) p_{y}-(\cos (ry) \sin (rx)) p_{z} \end{array}\right]
上式为点对位姿的雅可比,乘以残差对点的雅可比(coeff.x,coeff.y,coeff.z),得到对应代码中:
// 进行 ZXY 外旋定义坐标系下的雅可比计算
float arx = (crx*sry*srz*pointOri.x + crx*crz*sry*pointOri.y - srx*sry*pointOri.z) * coeff.x
+ (-srx*srz*pointOri.x - crz*srx*pointOri.y - crx*pointOri.z) * coeff.y
+ (crx*cry*srz*pointOri.x + crx*cry*crz*pointOri.y - cry*srx*pointOri.z) * coeff.z;
点对ry求雅可比有:
\frac{\partial(\boldsymbol{R} \boldsymbol{p})}{\partial ry}=\left[\begin{array}{c} (-\sin (ry) \cos (rz)+\cos (ry) \sin (rx) \sin (rz)) p_{x}+(\cos (rz) \cos (ry) \sin (rx)+\sin (ry) \sin (rz)) p_{y}+(\cos (rx) \cos (ry)) p_{z} \\ 0 \\ (-\sin (ry) \sin (rx) \sin (rz)-\cos (rz) \cos (ry)) p_{x}+(-\sin (ry) \cos (rz) \sin (rx)+\cos (ry) \sin (rz)) p_{y}-(\sin (ry) \cos (rx)) p_{z} \end{array}\right]
对应代码中:
float ary = ((cry*srx*srz - crz*sry)*pointOri.x
+ (sry*srz + cry*crz*srx)*pointOri.y + crx*cry*pointOri.z) * coeff.x
+ ((-cry*crz - srx*sry*srz)*pointOri.x
+ (cry*srz - crz*srx*sry)*pointOri.y - crx*sry*pointOri.z) * coeff.z;
点对rz求雅可比有:
\frac{\partial(\boldsymbol{R} \boldsymbol{p})}{\partial rz}=\left[\begin{array}{c} (-\cos (ry) \sin (rz)+\sin (ry) \sin (rx) \cos (rz)) p_{x}+(-\sin (rz) \sin (ry) \sin (rx)-\cos (ry) \cos (rz)) p_{y} \\ (\cos (rx) \cos (rz)) p_{x}-(\cos (rx) \sin (rz)) p_{y} \\ (\cos (ry) \sin (rx) \cos (rz)+\sin (rz) \sin (ry)) p_{x}+(-\cos (ry) \sin (rz) \sin (rx)+\sin (ry) \cos (rz)) p_{y} \end{array}\right]
对应代码中:
float arz = ((crz*srx*sry - cry*srz)*pointOri.x + (-cry*crz-srx*sry*srz)*pointOri.y)*coeff.x
+ (crx*crz*pointOri.x - crx*srz*pointOri.y) * coeff.y
+ ((sry*srz + cry*crz*srx)*pointOri.x + (crz*sry-cry*srx*srz)*pointOri.y)*coeff.z;
至此雅可比推导完毕,接下来构建方程进行求解
J^{T} J \Delta x=-J \cdot f(x)
对应代码中:
matA.at<float>(i, 0) = arz;
matA.at<float>(i, 1) = arx;
matA.at<float>(i, 2) = ary;
matA.at<float>(i, 3) = coeff.z;
matA.at<float>(i, 4) = coeff.x;
matA.at<float>(i, 5) = coeff.y;
matB.at<float>(i, 0) = -coeff.intensity;
// QR 分解求解 Hx=b
cv::transpose(matA, matAt);
matAtA = matAt * matA;
matAtB = matAt * matB;
cv::solve(matAtA, matAtB, matX, cv::DECOMP_QR);
更新位姿优化增量:
/// 更新当前关键帧全局位姿估计
transformTobeMapped[0] += matX.at<float>(0, 0);
transformTobeMapped[1] += matX.at<float>(1, 0);
transformTobeMapped[2] += matX.at<float>(2, 0);
transformTobeMapped[3] += matX.at<float>(3, 0);
transformTobeMapped[4] += matX.at<float>(4, 0);
transformTobeMapped[5] += matX.at<float>(5, 0);
参考:
1、https://blog.csdn.net/weixin_37835423/article/details/111587379
2、https://zhuanlan.zhihu.com/p/57351961
3、基于 LOAM 的方法中平面点和边缘线的残差构建以及雅可比推导
4、wykxwyc的博客 | wykxwyc&#39;s Blog |
|