|
|
理论上已经覆盖了高联平面几何的纯几何知识点
总算更新完了_(:3]z)_ (已躺平)
一、共点/共线
Menelaus定理
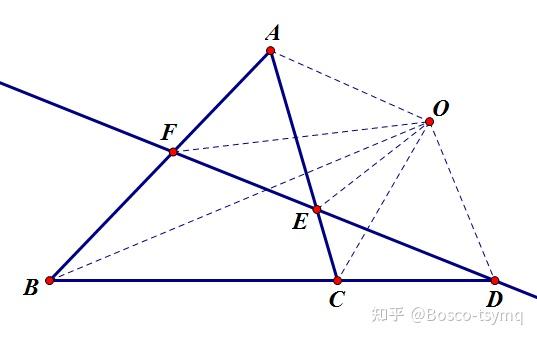
直线 DEF 与 \triangle ABC 的三边 BC,CA,AB 或它们的延长线分别相交于点 D,E,F ,则 \frac{AF}{FB}\cdot\frac{BD}{DC}\cdot\frac{CE}{EA}=1
第一角元形式: \frac{\sin\angle ACF}{\sin\angle FCB}\cdot\frac{\sin\angle BAD}{\sin\angle DAC}\cdot\frac{\sin\angle CBE}{\sin\angle EBA}=1
第二角元形式: \frac{\sin\angle AOF}{\sin\angle FOB}\cdot\frac{\sin\angle BOD}{\sin\angle DOC}\cdot\frac{\sin\angle COE}{\sin\angle EOA}=1
Ceva定理
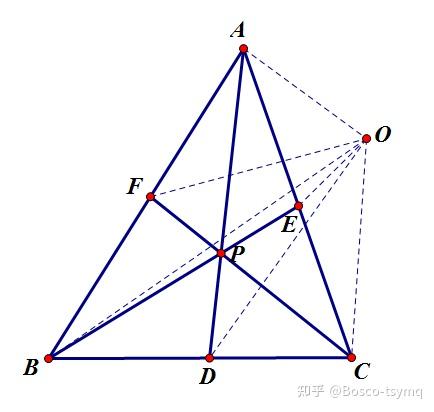
平面内任取一点 P ,直线 AP,BP,CP 分别于 \triangle ABC 的三边 BC,CA,AB 交于点 D,E,F ,则 \frac{AF}{FB}\cdot\frac{BD}{DC}\cdot\frac{CE}{EA}=1
第一角元形式: \frac{\sin\angle ACF}{\sin\angle FCB}\cdot\frac{\sin\angle BAD}{\sin\angle DAC}\cdot\frac{\sin\angle CBE}{\sin\angle EBA}=1
第二角元形式: \frac{\sin\angle AOF}{\sin\angle FOB}\cdot\frac{\sin\angle BOD}{\sin\angle DOC}\cdot\frac{\sin\angle COE}{\sin\angle EOA}=1
张角定理
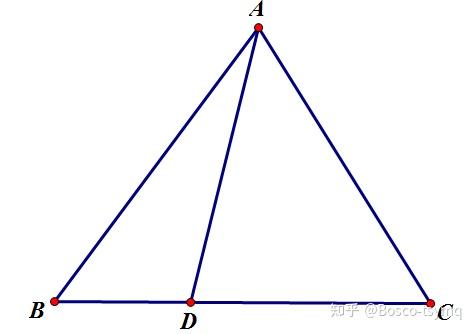
在△ABC中,D是BC上的一点,则 \frac{\sin\angle BAD}{AC}+\frac{\sin\angle CAD}{AB}=\frac{\sin\angle BAC}{AD}
Stewart定理

在△ABC中,D是BC上的一点,则 AD^2=\frac{AC^2\cdot BD+AB^2\cdot DC}{BC}-BD\cdot DC
中线长公式: m_a^2=\frac{1}{2}AB^2+\frac{1}{2}AC^2-\frac{1}{4}BC^2
角平分线长公式:
t_a=\frac{2}{AB+AC}\cdot\sqrt{AB\cdot AC \cdot p\cdot (p-BC)}\quad(p=\frac{BC+AC+AB}{2})
t_a=AB\cdot AC-BD\cdot DC
Desargues定理
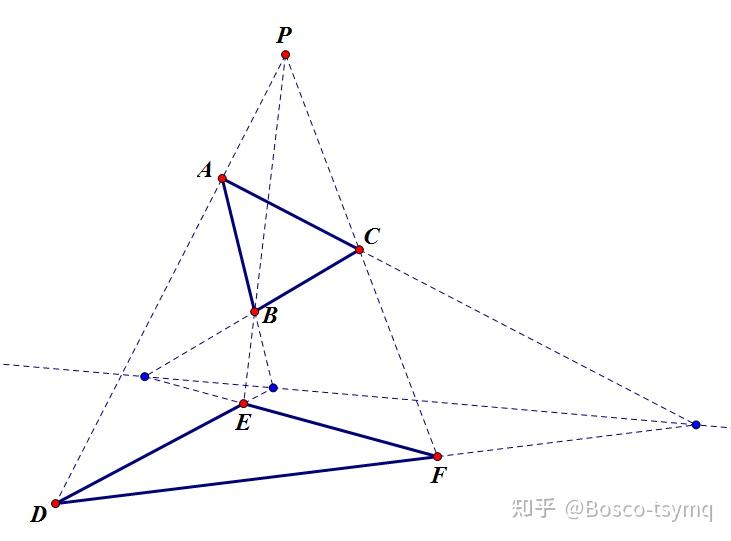
平面上有两个三角形 \triangle ABC,\triangle DEF,设它们的对应顶点( A 和 D 、 B 和 E 、 C 和 F )的连线交于一点,如果对应边或其延长线相交,则这三个交点共线
(以上逆定理均成立,可用来证明共线或共点)
Pascal定理
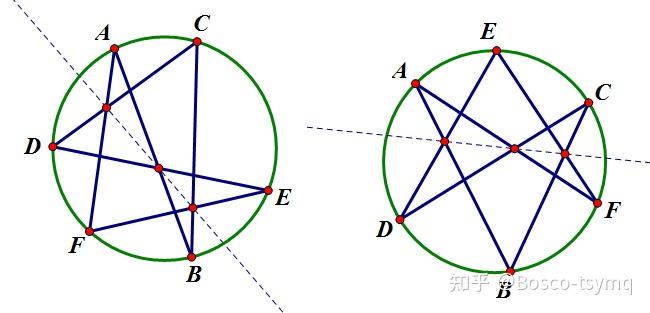
圆内接广义六边形 ABCDEF 三组对边的交点共线
Pappus定理
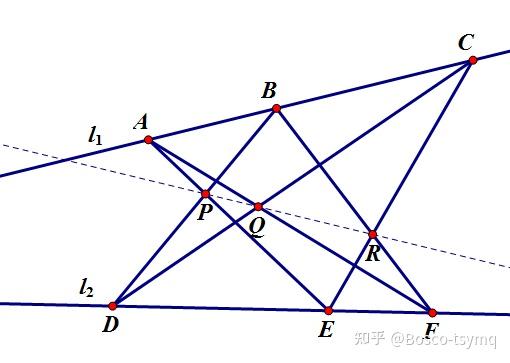
直线 l1 上依次有点 A,B,C ,直线 l2 上依次有点 D,E,F ,设 AE,BD 交于 P , AF,DC 交于 Q , BF,EC 交于 R ,则 P,Q,R 共线
Simson定理
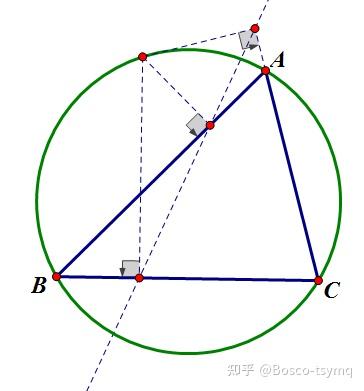
过三角形外接圆上异于三角形顶点的任意一点作三边或其延长线上的垂线,则三垂足共线
Newton定理
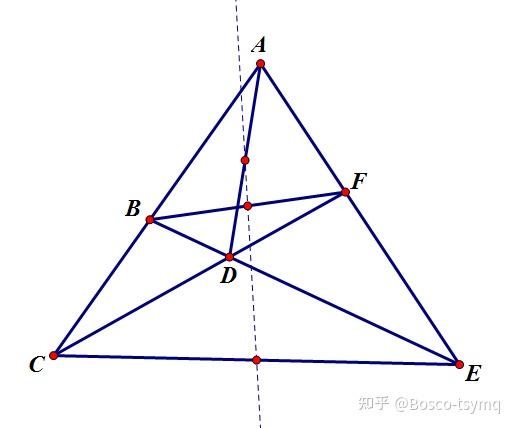
形式一:完全四边形三条对角线的中点共线
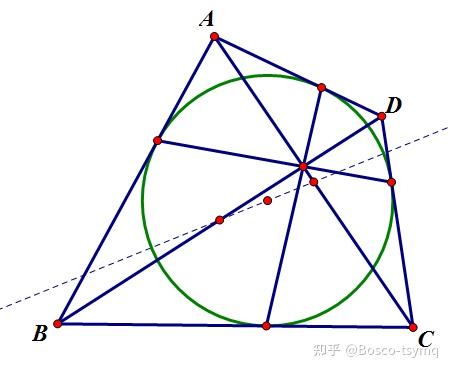
形式二:圆外切四边形两条对角线的中点和圆心共线
形式三:圆外切四边形两条对角线和切点四边形两条对角线四线共点
二、三角形
外心
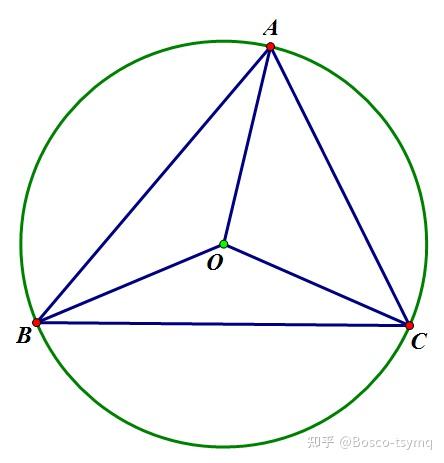
三角形外接圆的圆心,三边垂直平分线的交点
性质1:
\begin{align} O是\triangle ABC外心&\Leftrightarrow OA=OB=OC\\ &\Leftrightarrow OB=OC 且\angle BOC=2\angle BAC\\ &\Leftrightarrow \angle COA=2\angle CBA 且\angle BOC=2\angle BAC\\ \end{align}
性质2:
\sin 2A\cdot\vec{OA}+\sin 2B\cdot\vec{OB}+\sin 2C\cdot\vec{OC}=\vec{0}
内心
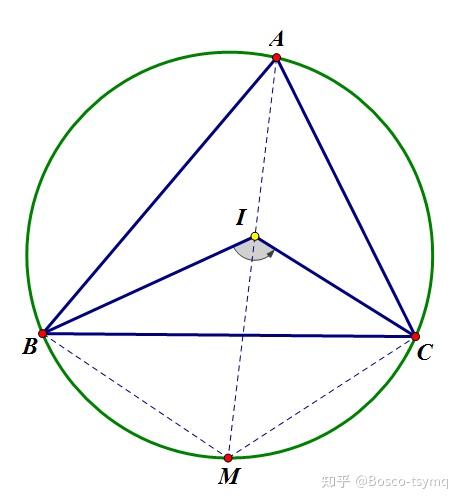
三角形内切圆的圆心,三条角平分线的交点
性质1:(内心张角)
\angle BIC=90^\circ+\frac{1}{2}\angle A
性质2:(鸡爪定理)
三角形一内角的平分线与其外接圆的交点到其它两顶点的距离及到内心的距离相等
即 MB=MC=MI
性质3:
\sin A\cdot\vec{IA}+\sin B\cdot\vec{IB}+\sin C\cdot\vec{IC}=\vec{0}
性质4:
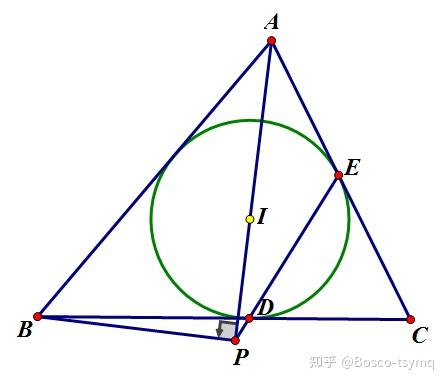
\triangle ABC 的内切圆切边 BC,CA 于点 D,E ,直线 AI 与 DE 交于点 P ,则 AP\bot BP
重心
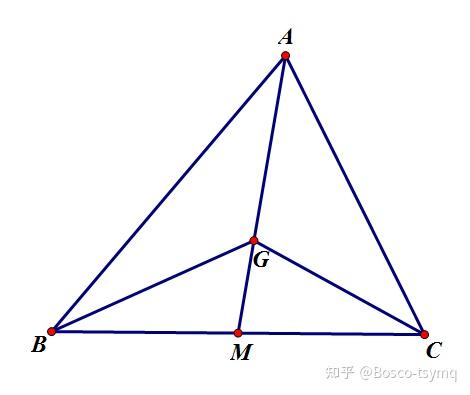
三角形三条中线的交点
性质1:
重心到顶点的距离与重心到对边中点的距离之比为 2:1 ,即 AG=2GM
性质2:
S_{\triangle AGB}=S_{\triangle BGC}=S_{\triangle CGA} ,即重心到三条边的距离与三边长成反比
性质3:
GA^2+GB^2+GC^2 最小
性质4:
在平面直角坐标系中, A(x_1,y_1),B(x_2,y_2),C(x_3,y_3) ,则 G(\frac{x_1+x_2+x_3}{3},\frac{y_1+y_2+y_3}{3})
性质5:
\vec{GA}+\vec{GB}+\vec{GC}=\vec{0}
垂心
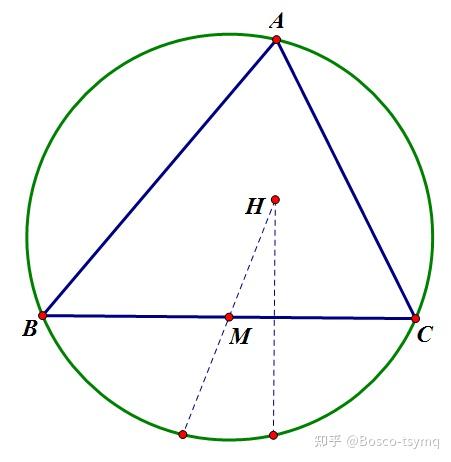
三角形三条高(所在直线)的交点
性质1:
(A,B,C,H) 构成一个垂心组,即其中一点是以另外三点为顶点的三角形的垂心
性质2:
垂心关于三边和三边中点的对称点在三角形外接圆上
性质3:
\tan A\cdot\vec{HA}+\tan B\cdot\vec{HB}+\tan C\cdot\vec{HC}=\vec{0}
旁心
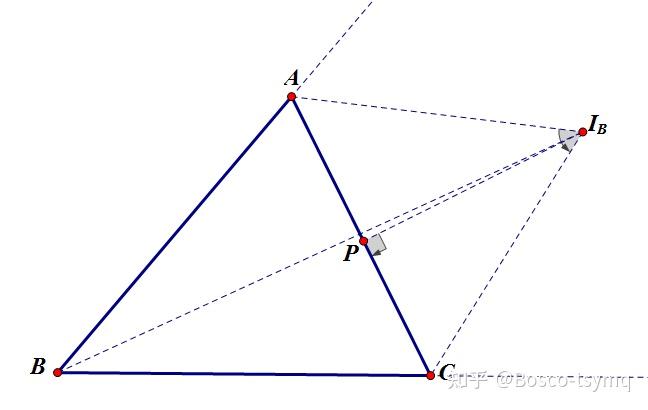
三角形旁切圆圆心,一内角平分线和另外两顶点处的外角平分线的交点
性质1:(旁心张角)
\angle AI_BC=90^\circ-\frac{1}{2}\angle B
性质2:
旁切圆在三角形三边上的切点是周长平分点,
即 AB+AP=CB+CP=\frac{AB+BC+CA}{2}
性质3:
\sin A\cdot\vec{I_BA}-\sin B\cdot\vec{I_BB}+\sin C\cdot\vec{I_BC}=\vec{0}
五心之间的一些结论
外心与垂心
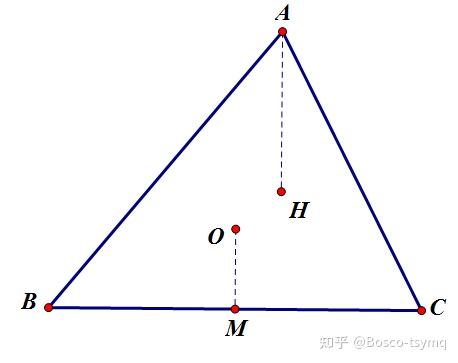
1、外心与垂心互为等角共轭点
2、垂心到三角形一顶点距离等于此三角形外心到此顶点对边距离的两倍,即 AH=2OM
Euler线
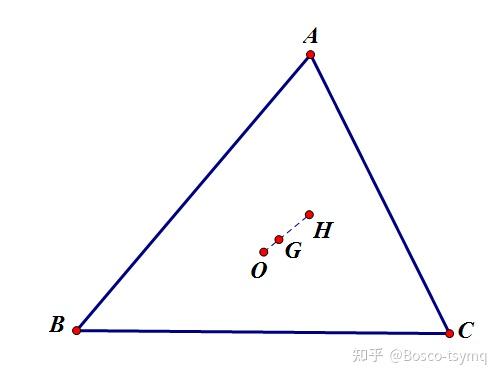
三角形外心、重心、垂心共线,且 GH=2OG
Euler定理
设三角形外接圆半径与内接圆半径分别为 R,r ,则 OI^2=R^2-2Rr
内心与旁心
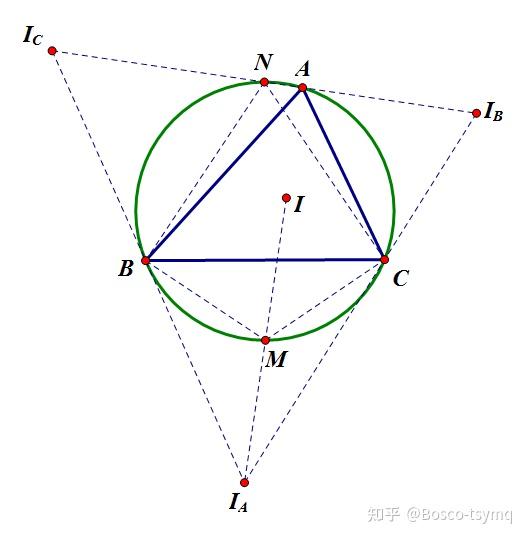
M 是 \triangle ABC 外接圆上 \mathop{BC}^\frown 的中点, N 是三角形外接圆上关于 M 的对径点
性质1:(鸡爪定理)
MB=MC=MI=MI_A
性质2:
(I,I_A,I_B,I_C) 构成一个垂心组
性质3:
NB=NC=NI_B=NI_C
实际上,三角形的外接圆正是旁心三角形的九点圆
九点圆
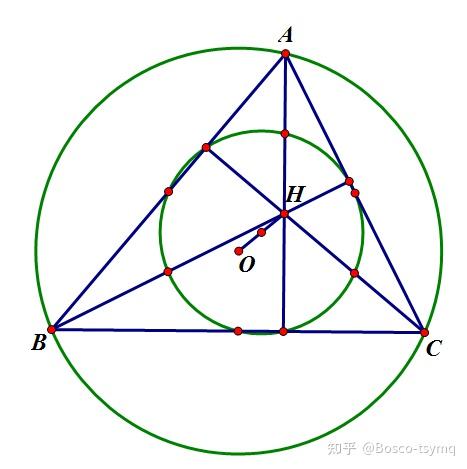
三角形垂心在三边上的投影、三边中点,三个顶点与垂心连线的中点九点共圆
性质1:
九点圆的圆心为 OH 中点,且九点圆半径为外接圆半径的一半
性质2:
九点圆与外接圆位似,位似比为 1:2
Steiner-Lehmus定理
若一个三角形的两个内角的角平分线相等,则该三角形必定为等腰三角形
三、圆
圆幂定理
Ptolemy定理
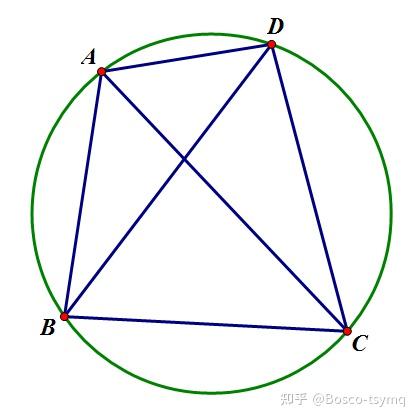
圆内接四边形两对对边乘积的和等于两条对角线的乘积,即 AB\times CD+AD\times BC=AC\times BD
推论1:
对任意凸四边形 ABCD , AB\times CD+AD\times BC\ge AC\times BD ,等号当且仅当四边形 ABCD 为圆内接四边形时成立
推论2:直线上的Euler定理
当圆退化成直线时, A,B,C,D 是直线上顺次的四点,则 AB\times CD+AD\times BC=AC\times BD
推广:开世定理*
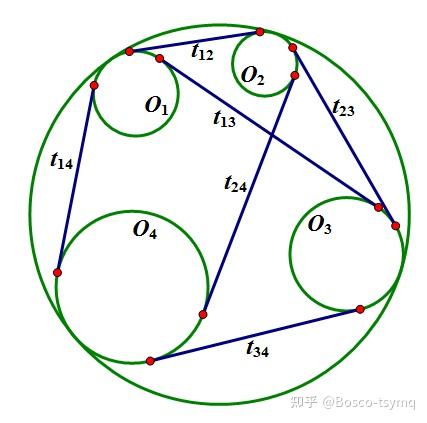
四个圆 O_1,O_2,O_3,O_4 相切于已知圆,如果将圆 O_i,O_j 的公切线的长度设为 t_{ij} (若同与已知圆外切或内切则为外公切线长,若一个与已知圆外切一个与已知圆内切则为内公切线长),那么 t_{12}t_{34}+t_{14}t_{23}=t_{13}t_{24}
其逆定理也成立,即若上式成立,则四个圆以规定的方式和已知圆相切
当开世定理中的四个圆退化成点时即为Ptolemy定理
根轴与根心
四、一些高级一点的东西*
调和点列与完全四边形
调和四边形与陪位中线
反演变换 |
|