|
|
如没看过一维的,见
仅供参考,若有出入,请以南大《声学基础》为准。欢迎指出,我将进行思考和修改。
<hr/>1. 声波方程的推导
1.1 基本假设
见声波—— 一维平面波(上)3.1节。
但是为了和大部分书籍符号匹配。小扰动假设有: \begin{aligned}P(\textbf{r},t)&=P_0+{p}(\textbf{r},t)\\ \rho(\textbf{r},t)&=\rho_0+{\rho&#39;}(\textbf{r},t)\\ T(\textbf{r},t)&=T_0+{\tau}(\textbf{r},t)\\ \textbf{V}(\textbf{r},t)&=\textbf{0}+{\textbf{v}}(\textbf{r},t)\end{aligned}\tag{1}
1.2 欧拉方程
三维的动量守恒见连续介质力学——基本守恒和平衡定律(下)公式5.17b,即 \begin{aligned}\nabla\cdot\boldsymbol{\sigma}+\rho\textbf{b}=\rho\dfrac{d\textbf{v}}{dt}=\rho\textbf{a}\quad\forall\textbf{x}\in V,\forall t\end{aligned}\\ 在声学中外力为压强,第一项可以化简为 -\nabla p 。因为此处不考虑源(体积力为0),所以第二项为0。并运用连续介质力学——运动的描述的(1.13)式,所以有 \begin{aligned}-\nabla P=\rho\dfrac{d\textbf{V}}{dt} = \left(\frac{\partial \mathbf{V}}{\partial t}+\mathbf{V}\cdot(\nabla\mathbf{V})\right) \end{aligned}\\ 因为小扰动假设(1),上式可以化为 \begin{aligned}\rho_0\dfrac{\partial\textbf{v}}{\partial t} +\nabla P = 0 \end{aligned}\tag{2}
1.3 质量守恒方程
三维的质量守恒见连续介质力学——基本守恒和平衡定律(上)的(5.9)式,即 \frac{\partial\rho}{\partial t}+\nabla\cdot\left(\rho\textbf{v}\right)=0\\ 因为小扰动假设(1),上式可以化为 \frac{\partial\rho&#39;}{\partial t}+\rho_0\nabla\cdot\textbf{v}=0\tag{3}
1.4 状态方程
见声波—— 一维平面波(补充篇)的2.4节或者声波—— 一维平面波(上)的3.4节,即 p=c_0^2\rho&#39;\tag{4} 其中c_0=\sqrt{\frac{\gamma P_0}{\rho_0}}是声音在空气(理想气体)中传播的速度。
1.5 声波方程
对(2)求散度, \nabla\cdot (2) 。将(4)代入(3)并对其求时间偏导, \frac{\partial}{\partial t}[(3)+(4)] 。参考声波—— 一维平面波(上)3.5节过程。可以得到声波方程 \Delta p -\frac{1}{c_0^2}\frac{\partial^2 p}{\partial t^2} = 0\tag{5} 其中 \begin{align} c_0^2 &= \frac{\gamma P_0}{\rho_0} = \frac{\gamma RT_0}{M}\\ \Delta p &= \frac{\partial^2 p}{\partial x^2}+\frac{\partial^2 p}{\partial y^2}+\frac{\partial^2 p}{\partial z^2} \end{align}\\
2. 声波方程的解
理论推导比较繁琐,推荐结合例题来学习。
2.1 通解
我们有三维的波动方程 \left(\frac{\partial^{2}}{\partial x^{2}}+\frac{\partial^{2}}{\partial y^{2}}+\frac{\partial^{2}}{\partial z^{2}}-\frac{1}{c_{o}^{2}}\frac{\partial^{2}}{\partial t^{2}}\right)p(x,y,z,t)=0,\quad\forall x,y,z,t.\tag{5} 它的通解为 p\left(x,y,z,t\right)=H\left(u\right)\tag{6a} 其中 u\left(x,y,z,t\right)=\alpha\left(t\pm\frac{x}{c_x}\pm\frac{y}{c_y}\pm\frac{z}{c_z}\right)+\beta\tag{6b}
且具有关系 \frac{1}{c_{o}^{2}}=\frac{1}{c_{x}^{2}}+\frac{1}{c_{y}^{2}}+\frac{1}{c_{z}^{2}}\tag{6c}
证明如下:
我们分析对 x 的偏导,即 \begin{align} \frac{\partial p}{\partial x}&=\frac{\partial\left(H\left(u\right)\right)}{\partial x}=\frac{\partial\left(H\left(u\right)\right)}{\partial u}\frac{\partial u}{\partial x}=\pm\frac{\alpha}{c_{x}}\frac{\partial\left(H\left(u\right)\right)}{\partial u}=\pm\frac{\alpha}{c_{x}}\frac{\partial p}{\partial u}\\ \frac{\partial^{2}p}{\partial x^{2}}&=\frac{\partial^{2}\left(H\left(u\right)\right)}{\partial x^{2}}=\frac{\partial\left(\pm\frac{\alpha}{c_{x}}\frac{\partial H\left(u\right)}{\partial u}\right)}{\partial u}\frac{\partial u}{\partial x}=\left(\frac{\alpha}{c_{x}}\right)^{2}\frac{\partial^{2}\left(H\left(u\right)\right)}{\partial u^{2}}=\left(\frac{\alpha}{c_{x}}\right)^{2}\frac{\partial^{2}p}{\partial u^{2}}. \end{align}\\ 同理可得 y,z 的偏导, \frac{\partial^{2}p}{\partial y^{2}}=\left(\frac{\alpha}{c_{y}}\right)^{2}\frac{\partial^{2}p}{\partial u^{2}},\;\frac{\partial^{2}p}{\partial z^{2}}=\left(\frac{\alpha}{c_{z}}\right)^{2}\frac{\partial^{2}p}{\partial u^{2}}\\ 现在我们分析对 t 的偏导,即 \begin{align} \frac{\partial p}{\partial t}&=\frac{\partial\left(H\left(u\right)\right)}{\partial t}=\frac{\partial\left(H\left(u\right)\right)}{\partial u}\frac{\partial u}{\partial t}=\alpha\frac{\partial\left(H\left(u\right)\right)}{\partial u}=\alpha\frac{\partial p}{\partial u}\\ \frac{\partial^{2}p}{\partial t^{2}}&=\frac{\partial^{2}\left(H\left(u\right)\right)}{\partial t^{2}}=\frac{\partial\left(\alpha\frac{\partial\left(H\left(u\right)\right)}{\partial u}\right)}{\partial u}\frac{\partial u}{\partial t}=\alpha^{2}\frac{\partial^{2}\left(H\left(u\right)\right)}{\partial u^{2}}=\alpha^{2}\frac{\partial^{2}p}{\partial u^{2}} \end{align}\\ 因此将(5)写成 \begin{align} \left(\frac{\alpha}{c_{x}}\right)^{2}\frac{\partial^{2}p}{\partial u^{2}}+\left(\frac{\alpha}{c_{y}}\right)^{2}\frac{\partial^{2}p}{\partial u^{2}}+\left(\frac{\alpha}{c_{z}}\right)^{2}\frac{\partial^{2}p}{\partial u^{2}}-\frac{1}{c_{0}^{2}}\alpha^{2}\frac{\partial^{2}p}{\partial u^{2}}=0\\ \Rightarrow \left[\left(\frac{\alpha}{c_{x}}\right)^{2}+\left(\frac{\alpha}{c_{y}}\right)^{2}+\left(\frac{\alpha}{c_{z}}\right)^{2}-\left(\frac{\alpha}{c_{0}}\right)^{2}\right]\frac{\partial^{2}\left(H\left(u\right)\right)}{\partial u^{2}}=0\\ \Rightarrow \frac{1}{c_{o}^{2}}=\frac{1}{c_{x}^{2}}+\frac{1}{c_{y}^{2}}+\frac{1}{c_{z}^{2}} \end{align}\\
2.2 谐波分析下的通解
我们分析单频(角频率为 \omega_0 )下的声波方程的解,即 p\left(x,y,z,t\right)=H\left(u\right)=H\left(\alpha\left(t\pm\frac{x}{c_{x}}\pm\frac{y}{c_{y}}\pm\frac{z}{c_{z}}\right)+\beta\right)\\ 因为 \alpha,\beta 是任意常数,我们令 \alpha = 2\pi F_0 = \omega_0 ,上式可以改写成 p=H\left(\omega_0t\pm\frac{\omega_0}{c_x}x\pm\frac{\omega_0}{c_y}y\pm\frac{\omega_0}{c_z}z+\beta\right)=H\left(\omega_0t\pm k_x x\pm k_y y\pm k_z z+\beta\right)\\ 令 \mathbf{k} 为波数,上式可以写成 p=H\left(\omega_{0}t\pm\mathbf{k}\cdot\mathbf{r}+\beta\right)\\ 关系(6c)可以改写成 k^{2}=k_{x}^{2}+k_{y}^{2}+k_{z}^{2}\tag{7} 这就是平面波的色散关系dispersion relation。
根据分离变量法,见下小节,我们可以得到, H 函数的可能取值。即三角函数或者复指数函数。因此我们可以将(6a)改写为 \hat{p}\left(x,y,z,t\right)=\hat{A}e^{j\left(\omega_{o}t\pm k_{x}x\pm k_{y}y\pm k_{z}z\right)}\tag{8} 其中系数 \hat{A}=\left|A\right|e^{j\beta} 可以是任意复数。
这便是三维平面波。
2.3 分离变量法
三维的波动方程 \left(\frac{\partial^{2}}{\partial x^{2}}+\frac{\partial^{2}}{\partial y^{2}}+\frac{\partial^{2}}{\partial z^{2}}-\frac{1}{c_{o}^{2}}\frac{\partial^{2}}{\partial t^{2}}\right)p(x,y,z,t)=0,\quad\forall x,y,z,t.\tag{5} 假设它的通解可以写成如下形式 p\left(x,y,z,t\right)=X\left(x\right)Y\left(y\right)Z\left(z\right)T\left(t\right)\\ 代入(5)可以改写成 \underbrace{\frac{1}{X(x)} \frac{\partial^{2} X(x)}{\partial x^{2}}+\frac{1}{Y(y)} \frac{\partial^{2} Y(y)}{\partial y^{2}}+\frac{1}{Z(z)} \frac{\partial^{2} Z(z)}{\partial z^{2}}}_{-k^{2}}=\underbrace{\frac{1}{c_{0}^{2} T(t)} \frac{\partial^{2} T(t)}{\partial t^{2}}}_{-k^{2}}, \quad \forall x, y, z, t \\ 上式可以拆成两个方程 \begin{align} \frac{1}{c_{o}^{2}T\left(t\right)}\frac{\partial^{2}T\left(t\right)}{\partial t^{2}}&=-k^{2},\forall t\tag{9a}\\ \frac{1}{X\left(x\right)}\frac{\partial^{2}X\left(x\right)}{\partial x^{2}}+\frac{1}{Y\left(y\right)}\frac{\partial^{2}Y\left(y\right)}{\partial y^{2}}+\frac{1}{Z\left(z\right)}\frac{\partial^{2}Z\left(z\right)}{\partial z^{2}}&=-k^{2},\quad\forall x,y,z\tag{9b} \end{align}\\
上述第一个方程(9a)可以写成 \frac{\partial^{2}T\left(t\right)}{\partial t^{2}}+\omega_{o}^{2}T\left(t\right)=0,\quad\forall t\tag{10} 其中 \omega_{0}=k c_{0} 。因此有4种解, \begin{array}{r c l}{{T(t)}}&{{=}}&{{e^{+j\omega t}}}\\ {{T(t)}}&{{=}}&{{e^{-j\omega t}}}\\ {{T(t)}}&{{=}}&{{\cos(\omega t)}}\\ {{T(t)}}&{{=}}&{{\sin(\omega t)}}\end{array}\\ 这里我们选择第一种解 \begin{array}{ccc}T(t)&=&e^{+j\omega t}\end{array}\tag{11}
上述第二个方程(9b)可以写成 \begin{align} \underbrace{\frac{1}{X\left(x\right)}\frac{\partial^{2}X\left(x\right)}{\partial x^{2}}+\frac{1}{Y\left(y\right)}\frac{\partial^{2}Y\left(y\right)}{\partial y^{2}}+k^{2}}_{=k_{z}^{2}}=\underbrace{-\frac{1}{Z\left(z\right)}\frac{\partial^{2}Z\left(z\right)}{\partial z^{2}}}_{=k_{z}^{2}}\quad\forall x,y,z\\ \Rightarrow \frac{1}{X\left(x\right)}\frac{\partial^{2}X\left(x\right)}{\partial x^{2}}+\frac{1}{Y\left(y\right)}\frac{\partial^{2}Y\left(y\right)}{\partial y^{2}}+k^{2}-k_{z}^{2}=0\quad\forall x,\forall y\\ \text{和 }\frac{\partial^{2}Z\left(z\right)}{\partial z^{2}}+k_{z}^{2}Z\left(z\right)=0,\quad\forall z \end{align}\tag{12} 因此 Z(z) 有4种解,只需在其中任选两个线性组合。因为有一个波可以拆成左行波leftgoing wave和右行波rightgoing wave,见声波—— 一维平面波(上)的3.6节(8)式。 \begin{align} Z\left(z\right)&=e^{+j k_{z}z}\\ Z\left(z\right)&=e^{-j k_{z}z}\\ Z\left(z\right)&=\cos\left(k_{z}z\right)\\ Z\left(z\right)&=\sin\left(k_{z}z\right)\\ \end{align}\tag{13} 在式(12)的基础上继续改进,即 \begin{align} \underbrace{\frac{1}{X\left(x\right)}\frac{\partial^{2}X\left(x\right)}{\partial x^{2}}+k^{2}-k_{z}^{2}}_{=k_{y}^{2}}=\underbrace{\frac{1}{V\left(y\right)}\frac{\partial^{2}Y\left(y\right)}{\partial y^{2}}}_{=k_{y}^{2}}\quad \forall x,y\\ \Rightarrow \frac{1}{X\left(x\right)}\frac{\partial^{2}X\left(x\right)}{\partial x^{2}}+k^{2}-k_{z}^{2}-k_{y}^{2}=0\quad\forall x\\ \text{和 }\frac{\partial^{2}Y\left(y\right)}{\partial y^{2}}+k_{y}^{2}Y\left(y\right)=0\quad\forall y \end{align}\tag{14} 因此 Y(y) 有4种解,只需在其中任选两个线性组合。 \begin{align} Y\left(y\right)&=e^{+j k_{y}y}\\ Y\left(y\right)&=e^{-j k_{y}y}\\ Y\left(y\right)&=\cos\left(k_{y}y\right)\\ Y\left(y\right)&=\sin\left(k_{y}y\right)\\ \end{align}\tag{15} 在式(14)的基础上继续改进,即 \frac{1}{X\left(x\right)}\frac{\partial^{2}X\left(x\right)}{\partial x^{2}}=-k^{2}+k_{z}^{2}+k_{y}^{2}=-k_{x}^{2}\quad\forall x\tag{16} 因此 X(x) 有4种解,只需在其中任选两个线性组合。 \begin{align} X\left(x\right)&=e^{+j k_{x}x}\\ X\left(x\right)&=e^{-j k_{x}x}\\ X\left(x\right)&=\cos\left(k_{x}x\right)\\ X\left(x\right)&=\sin\left(k_{x}x\right)\\ \end{align}\tag{17}
总结一下,三维的波动方程的解为 p\left(x,y,z,t\right)=X\left(x\right)Y\left(y\right)Z\left(z\right)T\left(t\right)\tag{18} 其中 X\left(x\right),Y\left(y\right),Z\left(z\right) 分别为(17),(15),(13)式中任选两个进行线性组合。 T\left(t\right) 为(11)式。
2.4 模态分析与隐失波evanescent
见下一章。
3. 例题
我们分析一个长方形的无限长管里的声场。管的方向为 z 轴,管的墙壁都是完全反射的硬墙。现在有一个沿着 z 正向传播的声,试求出其压强。
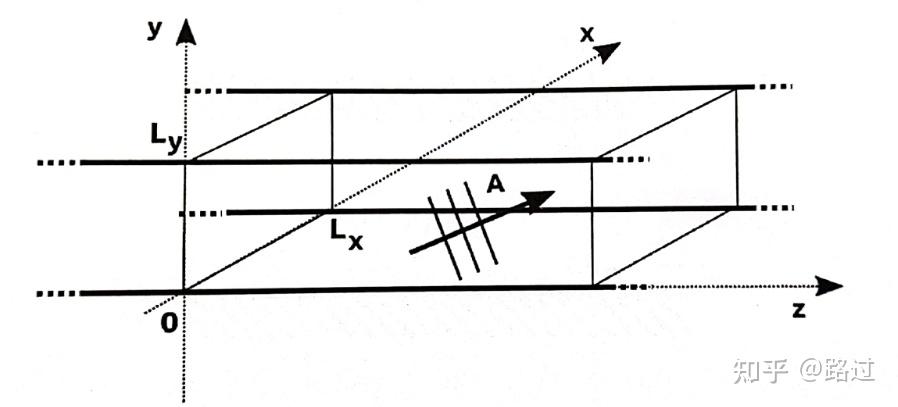
图1. 长方形的无限长管
3.1 死板的解法
我们可以列出声波方程 (\Delta + k^2)p(\mathbf{r}) = 0\quad \forall \mathbf{r}\in \mathcal{D}\\ 其中 \mathcal{D} = \{0\le x\le L_x,0\le y\le L_y, \forall z\} 。
其边界条件为 \begin{align} -\left.\frac{\partial p}{\partial x}\right|_{x=0} &= 0\quad (x=0的\text{yoz}平面上的墙)\\ \left.\frac{\partial p}{\partial x}\right|_{x=L_x} &= 0\quad (x=L_x的\text{yoz}平面上的墙)\\ -\left.\frac{\partial p}{\partial y}\right|_{y=0} &= 0\quad (y=0的\text{xoz}平面上的墙)\\ \left.\frac{\partial p}{\partial y}\right|_{y=L_y} &= 0\quad (y=L_y的\text{xoz}平面上的墙) \end{align}\\ 我们因为无限长管,所以不考虑 z 轴反射波。因此可以分解成4个方向的波( x 轴2个, y 轴两个,即 2\times 2 )其分别为 \begin{align} p = &Ae^{-jk^A_xx}e^{-jk^A_yy}e^{-jk^A_zz}e^{j\omega t}\quad &x^+y^+z^+方向\\ &+Be^{jk^B_xx}e^{-jk^B_yy}e^{-jk^B_zz}e^{j\omega t}\quad &x^-y^+z^+方向\\ &+Ce^{-jk^C_xx}e^{jk^C_yy}e^{-jk^C_zz}e^{j\omega t}\quad &x^+y^-z^+方向\\ &+De^{jk^D_xx}e^{jk^D_yy}e^{-jk^D_zz}e^{j\omega t}\quad &x^-y^-z^+方向 \end{align}\\ 因为介质没有变化,所以 k_i^A = k_i^B = k_i^C =k_i^D\quad i\in\{x,y,z\} 。
根据边界条件,我们有以下4个方程式 \begin{align} (-A+B)e^{-jk_y y}+(-C+D)e^{jk_yy} &= 0\\ (-Ae^{-jk_xL_x}+Be^{jk_xL_x})e^{-jk_y y}+(-Ce^{-jk_xL_x}+De^{jk_xL_x})e^{jk_yy} &= 0\\ (-A+C)e^{-jk_x x}+(-B+D)e^{jk_xx} &= 0\\ (-Ae^{-jk_y L_y}+Ce^{jk_y L_y})e^{-jk_xx}+(-Be^{-jk_y L_y}+De^{jk_y L_y})e^{jk_xx} &= 0 \end{align}\\ 因此可以得到 \begin{align} A=B,C&=D\\ \sin k_xL_x &= 0\Rightarrow k_x = \frac{n_x\pi}{L_x}\\ A=C,B&=D\\ \sin k_yL_y&=0\Rightarrow k_y = \frac{n_y\pi}{L_y} \end{align}\\ 所以声波方程可以写成 \begin{align} p &= A\left(e^{-jk_xx}e^{-jk_yy}+e^{jk_xx}e^{-jk_yy}+e^{-jk_xx}e^{jk_yy}+e^{jk_xx}e^{jk_yy}\right)e^{-jk_zz}e^{i\omega t}\\ &=A\left(2\cos (k_xx)e^{-jk_yy}+2\cos (k_xx) e^{jk_yy}\right)e^{-jk_zz}e^{j\omega t}\\ &= A\cos (k_xx) \cos (k_yy) e^{-jk_zz}e^{j\omega t} \end{align}\\
注意:因为 A 是任意常数,可以将 4 并入其中。
3.2 灵活的解法
因为三维的波动方程的解(18)中X\left(x\right),Y\left(y\right),Z\left(z\right) 分别为(17),(15),(13)式里选择,所以我们可以直接假设声波方程的解为 p = \left(A\cos(k_xx)+B\sin(k_xx)\right)\left(C\cos(k_yy)+D\sin(k_yy)\right)e^{-jk_zz}e^{j\omega t}\\ 同样其边界条件为 \begin{align} -\left.\frac{\partial p}{\partial x}\right|_{x=0} &= 0\quad (x=0的\text{yoz}平面上的墙)\\ \left.\frac{\partial p}{\partial x}\right|_{x=L_x} &= 0\quad (x=L_x的\text{yoz}平面上的墙)\\ -\left.\frac{\partial p}{\partial y}\right|_{y=0} &= 0\quad (y=0的\text{xoz}平面上的墙)\\ \left.\frac{\partial p}{\partial y}\right|_{y=L_y} &= 0\quad (y=L_y的\text{xoz}平面上的墙) \end{align}\\ 代入可得 \begin{align} B &=0\\ \sin(k_xL_x) &= 0\Rightarrow k_x = \frac{n_x\pi}{L_x}\\ D&=0\\ \sin(k_yL_y) &= 0\Rightarrow k_y = \frac{n_y\pi}{L_y} \end{align}\\ 因此可以 p= A\cos (k_xx) \cos (k_yy) e^{-jk_zz}e^{j\omega t}\\ 注意:因为 A,C 是任意常数,所以可以合并。
3.3 模态分析
我们可以观察发现因为 k_x,k_y 有无数个值,所以声压也有无数个解。我们可以将上式(声压的解)写成如下形式 p_{n_xn_y} = A\Psi_{n_xn_y}(x,y)e^{-jk_zz}e^{j\omega t}\\ 其中 \Psi_{n_xn_y}(x,y) = \cos \left(\frac{n_x \pi}{L_x}x\right) \cos \left(\frac{n_y \pi}{L_y}y\right) 。而总声压便是将所有声压解加和起来,即 p_{tot} = \sum\limits_{n_x,n_y=0}\limits^{\infty}p_{n_xn_y}\\ 其中任意一个解 p_{n_xn_y} 便称为模态声压。
我们首先分析模态(0,0)的情况,即 n_x = 0,n_y=0 。模态声压为p_{(0,0)} = Ae^{-jk_zz}e^{j\omega t}\\ 其声压为常数与 x,y 无关。
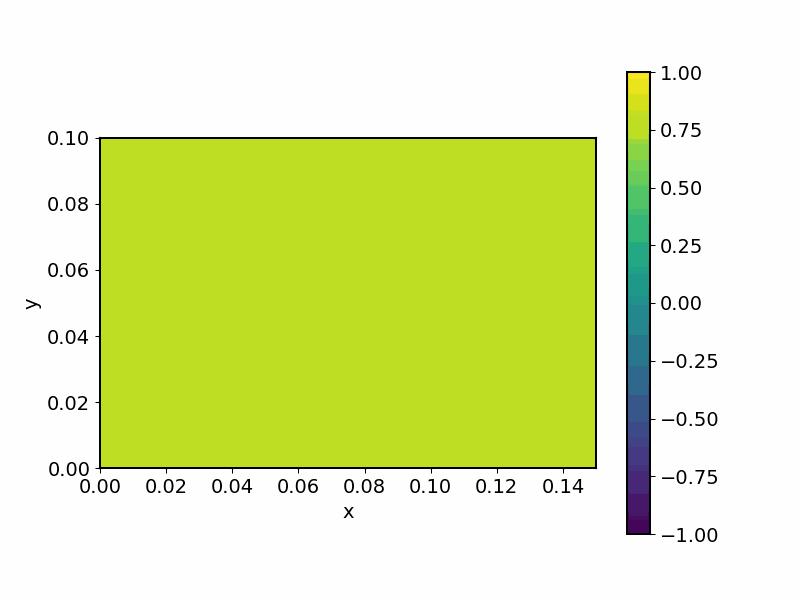
图2. 模态(0,0)下的任意一点z的压强随时间变化图
分析模态(1,0)的情况,即 n_x = 1,n_y=0 。模态解和模态声压为 \Psi_{(1,0)}(x,y) = \cos\left(\frac{\pi}{L_x}x\right),\; p_{(1,0)} = A_{(1,0)}\cos\left(\frac{\pi}{L_x}x\right)e^{-jk_zz}e^{j\omega t}\\
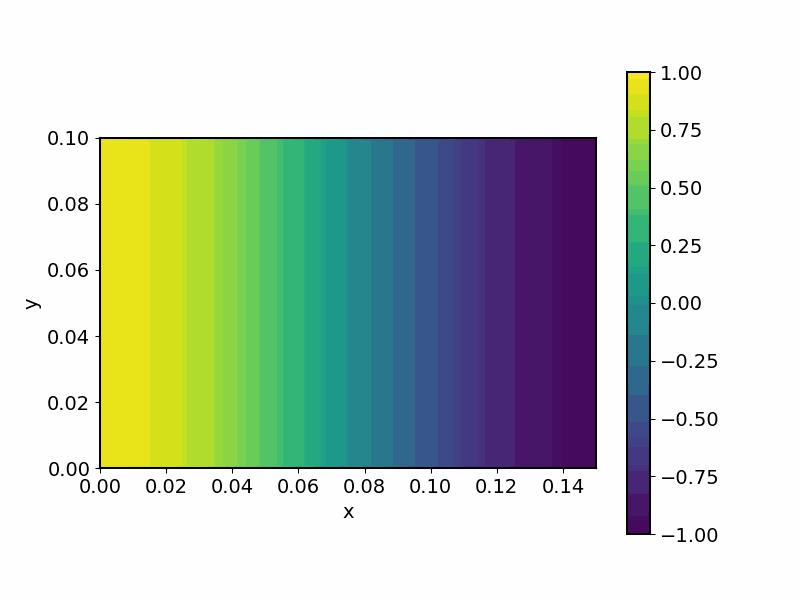
图3. 模态(1,0)下的任意一点z的压强随时间变化图
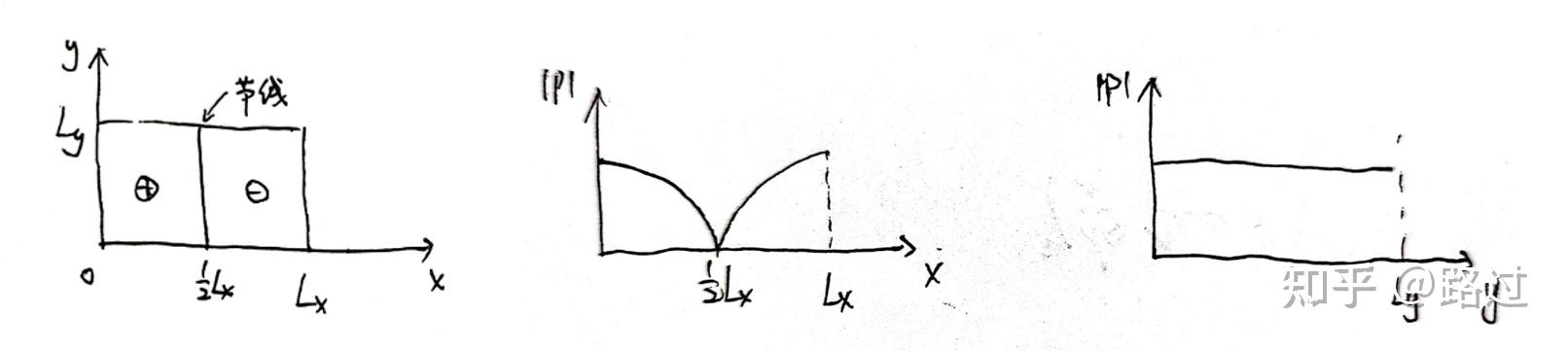
图4. 模态(1,0)
分析模态(0,2)的情况,即 n_x = 0,n_y=2 。模态解和模态声压为 \Psi_{(0,2)}(x,y) = \cos\left(\frac{2\pi}{L_y}y\right),\; p_{(0,2)} = A_{(0,2)}\cos\left(\frac{2\pi}{L_y}y\right)e^{-jk_zz}e^{j\omega t}\\
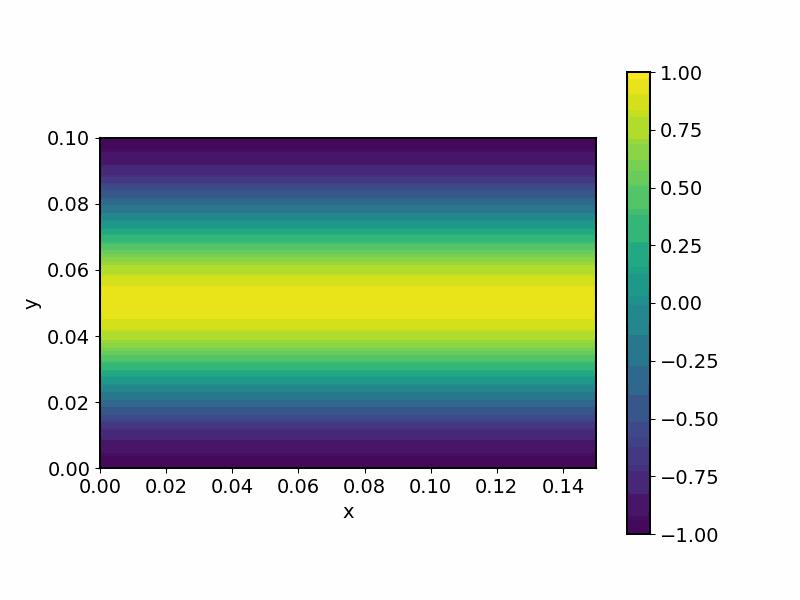
图5. 模态(0,2)下的任意一点z的压强随时间变化图
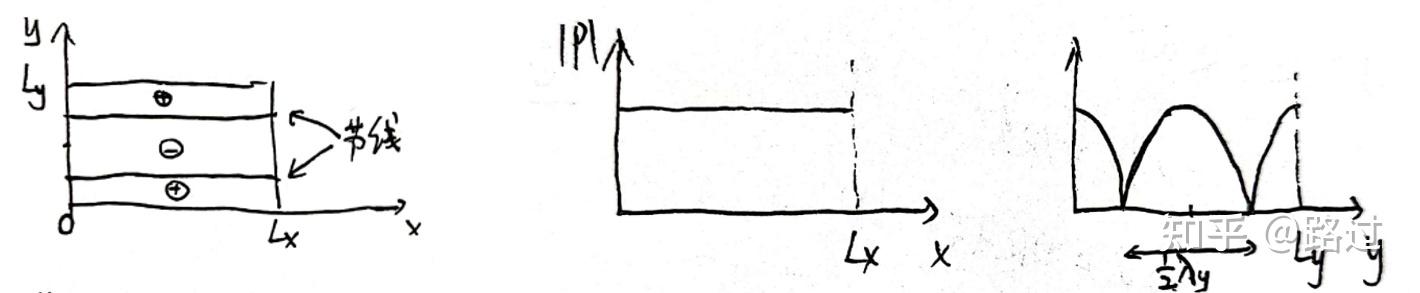
图6. 模态(0,2)
分析模态(1,1)的情况,即 n_x = 1,n_y=1 。模态解和模态声压为 \Psi_{(1,1)}(x,y) = \cos\left(\frac{\pi}{L_x}x\right)\cos\left(\frac{\pi}{L_y}y\right),\; \\p_{(1,1)} = A_{(1,1)}\cos\left(\frac{\pi}{L_x}x\right)\cos\left(\frac{\pi}{L_y}y\right)e^{-jk_zz}e^{j\omega t}\\
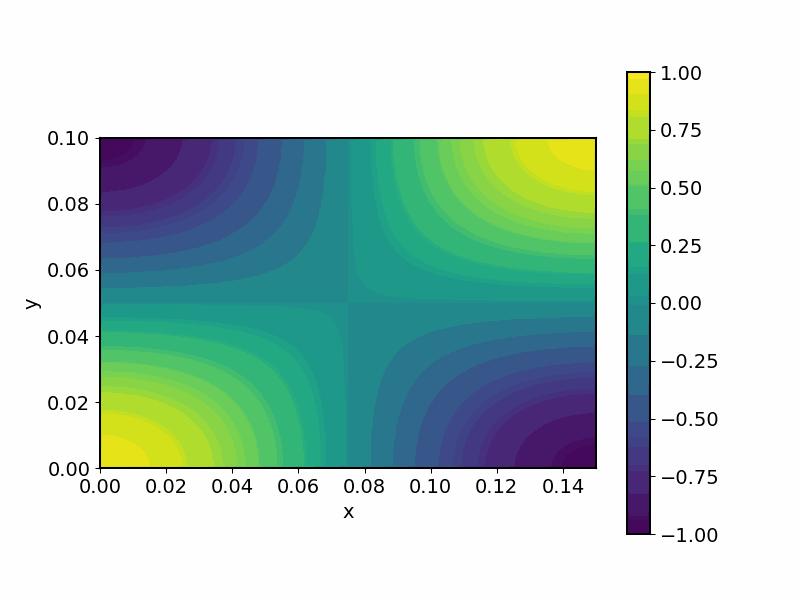
图7. 模态(1,1)下的任意一点z的压强随时间变化图
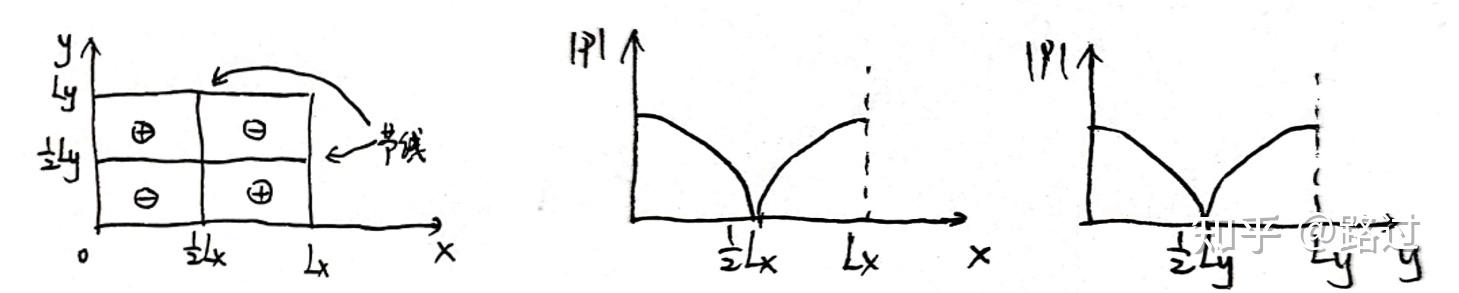
图8. 模态(1,1)
3.4 隐失波evanescent
关于隐失波evanescent的具体物理意义,会在之后的波动物理相关文章里进行分析。此处只做计算。
根据边界条件,我们还可以写出色散关系dispersion relation k_z^2 +\left(\frac{n_x \pi}{L_x}\right)^2 +\left(\frac{n_y \pi}{L_y}\right)^2 = \left(\frac{\omega}{c_0}\right)^2\\ 因此可以写出 k_z =\sqrt{\left(\frac{\omega}{c_0}\right)^2 - \left(\frac{n_x \pi}{L_x}\right)^2 - \left(\frac{n_y \pi}{L_y}\right)^2}\\ 如果 \left(\frac{n_x \pi}{L_x}\right)^2 +\left(\frac{n_y \pi}{L_y}\right)^2 > \left(\frac{\omega}{c_0}\right)^2 ,即 k_z 变成虚数,便是隐失波evanescent。
此时 k_z =\pm j\sqrt{\left(\frac{n_x \pi}{L_x}\right)^2 + \left(\frac{n_y \pi}{L_y}\right)^2-\left(\frac{\omega}{c_0}\right)^2} = \pm j \xi\\ 将其代入声压方程有 p_{n_xn_y} = A\Psi_{n_xn_y}(x,y)e^{\pm \xi z}e^{j\omega t}\\ 因为声波不会在无源传播时增幅增大,所以 k_z 的有物理意义的解为 k_z = j\sqrt{\left(\frac{n_x \pi}{L_x}\right)^2 + \left(\frac{n_y \pi}{L_y}\right)^2-\left(\frac{\omega}{c_0}\right)^2} = j \xi\\ 将其代入声压方程有 p_{n_xn_y} = A\Psi_{n_xn_y}(x,y)e^{-\xi z}e^{j\omega t}\\
也就是说在隐失波evanescent的情况下,声波会随着 z 的传播衰减(注意这不是声能耗散dissipation)。换句话说在模态下,存在一个模态截止频率, f_c = \frac{c_0}{2}\sqrt{\left(\frac{n_x}{L_x}\right)^2+\left(\frac{n_y}{L_y}\right)^2}\\ 当频率小于这个截止频率 f_c 时,这个模态不传播(存在,但是以evanescent的形式存在)。
<hr/>如果觉得对您有用,请点个赞,让更多人需要时能搜到。制作这么多公式和图片的像教材一样的半原创优质文章不易,请多多支持。你的点赞是我继续更新的动力。 |
|