|
|
前言
模板元编程如果之前有过了解,应该知道是利用C++的模板来在编译期进行一些运算。
属于是那种,感觉很厉害,但是实际上好像用不到。
实际上,在有了 constexpr 后,模板元编程确实没啥用了,不过用来学习模板还是可以的。
template<typename T>
T Max(T a, T b) {
return a > b ? a : b;
}
上面是一个简单的模板的示例。
这里我们需要明白一点 模板就是面向编译器的编程。
即 ,我们通过模板的编写来让编译器帮我们生成一些代码。
这里我们可以通过这个网站 C++ Insights 来查看模板展开后的结果。
例如
template<typename T>
T Max(T a, T b) {
return a > b ? a : b;
}
int main()
{
Max(3, 4);
Max(3.14, 11.5414);
}
展开成了
/* First instantiated from: insights.cpp:9 */
#ifdef INSIGHTS_USE_TEMPLATE
template<>
int Max<int>(int a, int b)
{
return a > b ? a : b;
}
#endif
/* First instantiated from: insights.cpp:10 */
#ifdef INSIGHTS_USE_TEMPLATE
template<>
double Max<double>(double a, double b)
{
return a > b ? a : b;
}
#endif
int main()
{
Max(3, 4);
Max(3.1400000000000001, 11.541399999999999);
return 0;
}
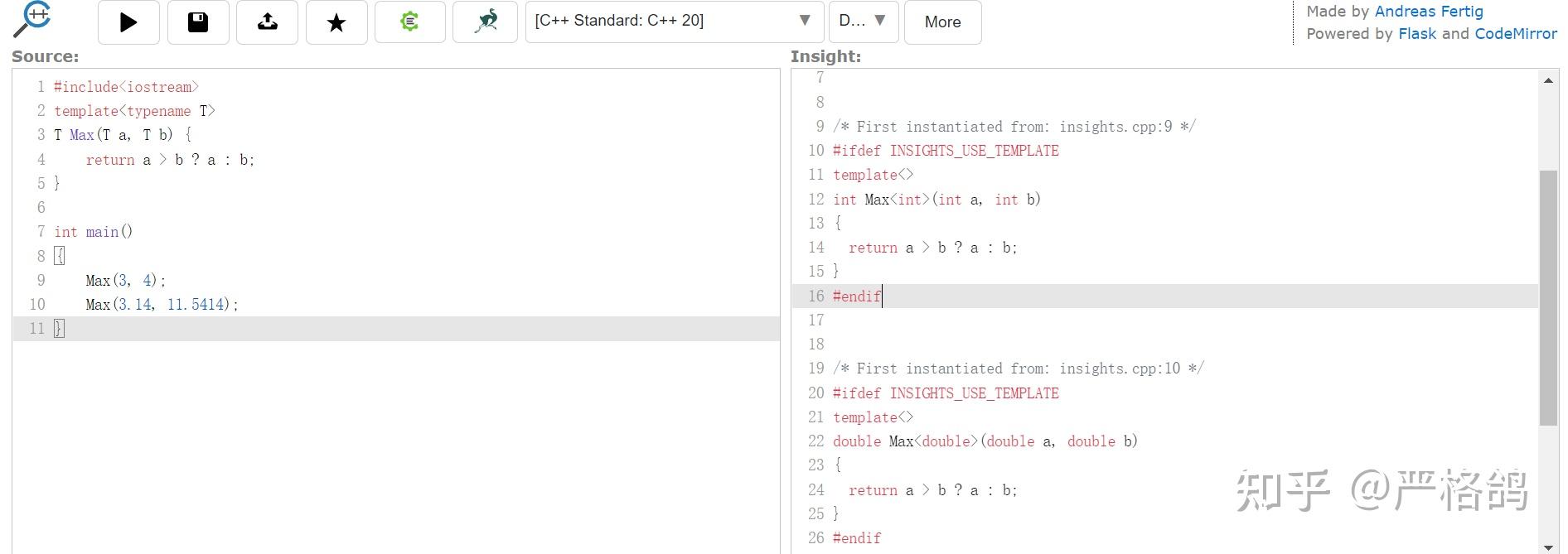
展开的行为就是模板的特化。
好,让我们开始模板元编程的第一步。
在编译期求阶乘
准备
既然是在编译期求的量,那么应该是一个常量,我们需要const 来修饰。
因为是编译期的数据,所以需要是static (这样就可以在编译期获得了。
所以我们先写出这样的格式。
template<int N>
struct Fac {
const static int value;
};
其中value 就是我们需要求的值。
然后我们可以这样,移动鼠标,利用IDE的编译器来访问数据
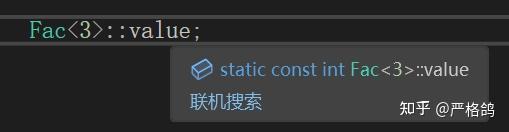
编写
根据阶乘的定义,我们可以写出这样的递归调用
template<int N>
struct Fac {
const static int value = N * Fac<N - 1>::value;
};
但是这样显然是不能出结果的(鼠标移动到上面会发现卡住了
因为既然是递归,就要有一个停下来的地方。
所以加上一句
template<int N>
struct Fac {
const static int value = N * Fac<N - 1>::value;
};
template<>
struct Fac<0> {
const static int value = 1;
};
这个时候可以发现
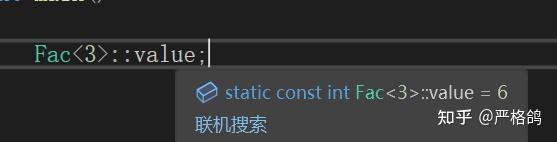
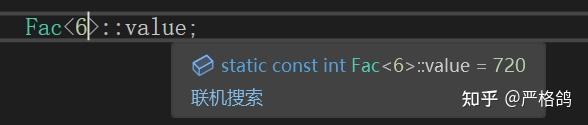
阶乘的值在编译期被计算出来了。
我们来看看Fac<3>的展开。
/* First instantiated from: insights.cpp:4 */
#ifdef INSIGHTS_USE_TEMPLATE
template<>
struct Fac<2>
{
static const int value = 2 * Fac<1>::value;
};
#endif
/* First instantiated from: insights.cpp:4 */
#ifdef INSIGHTS_USE_TEMPLATE
template<>
struct Fac<1>
{
static const int value = 1 * Fac<0>::value;
};
#endif
/* First instantiated from: insights.cpp:14 */
#ifdef INSIGHTS_USE_TEMPLATE
template<>
struct Fac<3>
{
static const int value = 3 * Fac<2>::value;
};
#endif
显然你是否有点理解模板就是面向编译器编程的这句话了呢?
编译期求斐波那契数列
根据上面的阶乘,很容易就可以写出斐波那契的代码
template<int N>
struct Fib {
const static int value = Fib<N - 1>::value + Fib<N - 2>::value;
};
template<>
struct Fib<1> {
const static int value = 1;
};
template<>
struct Fib<2> {
const static int value = 1;
};
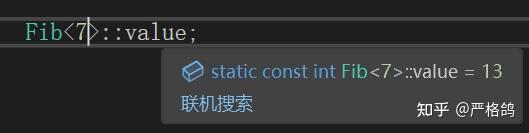
那么复杂度?
众所周知,斐波那契数列的递归求法的复杂度是 O(2^N) 的。
但是如果我们直接求第100项的话

可以发现编译期很快的就求出来了(负数是因为爆了int)
为什么会这么快呢?实际上,模板的展开只会展开一次。
例如Fac<6>

实际上展开成了
template<>
struct Fib<5>
{
static const int value = Fib<4>::value + Fib<3>::value;
};
template<>
struct Fib<4>
{
static const int value = Fib<3>::value + Fib<2>::value;
};
template<>
struct Fib<3>
{
static const int value = Fib<2>::value + Fib<1>::value;
};
template<>
struct Fib<6>
{
static const int value = Fib<5>::value + Fib<4>::value;
};
template<>
struct Fib<1>
{
static const int value = 1;
};
template<>
struct Fib<2>
{
static const int value = 1;
};
可以看到,每一种Fac<N> 都只展开了一次,并不会像我们认为的,递归重复的展开。
那么复杂度就是 O(N)
编译期求最大公约数
上面都是传递一个参数,这里多传递一个
template<int a, int b>
struct Gcd {
const static int value = Gcd<b, a% b>::value;
};
template<int a>
struct Gcd<a, 0> {
const static int value = a;
};


编译期条件判断
编译期的循环我们可以使用递归来完成,但是条件判断呢?
大致想象一个我们需要的IF
IF<
/*判断的条件*/,
/*为真的类型*/,
/*为假的类型*/
>
这里我们用一个讨巧的做法
template <bool flag, typename True, typename False>
struct IF {};
template<typename True, typename False>
struct IF<true, True, False> {
using ret = True;
};
template<typename True, typename False>
struct IF<false, True, False> {
using ret = False;
};
然后是真,我们就给True取个别名
来写一个样例,输入一个N,如果是奇数就输出阶乘,否则输出斐波那契数列。
template<int N>
struct Choose {
const static int value =
IF<
N % 2 == 1,
Fac<N>,
Fib<N>
>::ret::value;
};
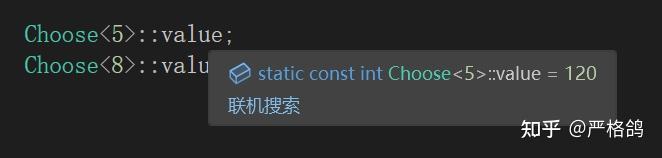

这里我们还需要引入一个东西,因为我们返回的ret都是需要一个value的属性。
为了让int也可以放进去,我们需要包装一下int
template<int N>
struct Int {
const static int value = N;
};
编译期判断质数
首先至少需要一个这个
IF<
(N% i == 0),
Int<0>,
is_Prime<i + 1, N>
>
优化一点就是我们只需要从2枚举到 \sqrt{N}
所以需要IF的嵌套
template<int i,int N>
struct is_Prime {
const static int value =
IF<
(i * i> N),
Int<1>,
IF<
( N% i == 0),
Int<0>,
is_Prime<i + 1,N>
>::ret
> ::ret::value;
};



计算1到N中有多少个质数
注意到其实上面的代码有一些问题
比如N = 1 的时候,直接判断i *i > N 了,所以特化一个
template<>
struct is_Prime<2,1> {
const static int value = 0;
};
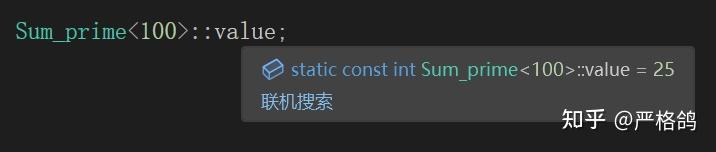
这样我们来计算1到N中有多少个质数
template<int N>
struct Sum_prime {
const static int value = is_Prime<2, N>::value + Sum_prime<N - 1>::value;
};
template<>
struct Sum_prime<0> {
const static int value = 0;
};

最后
当然,一个图灵完备的语言还需要有存储结构,也就是数组/列表这样的东西。
这部分的话,有一些不同的实现。
比如我比较喜欢用不定长参数来表示数组。
int main()
{
using list = Arr<1, 1, 4, 5, 1, 4>;
Sum<list>::value;//16
Find_max<list>::value;//5
At<list, 3>::value;//5
}
不过鉴于模板不定长参数可能有一部分读者不会,所以这里就不写了,等后面我自己写一个教程吧。 |
|