|
|
今天开始介绍空间中一些基本几何体的方程,介绍完了再来应用一哈.
Ⅰ.平面的基底与平面的参数方程
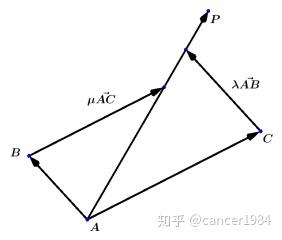
设平面中不共线三点为A(x_{1},y_{1},z_{1}),B(x_{2},y_{2},z_{2}),C(x_{3},y_{3},z_{3}),
则向量\overset{\rightarrow }{AB}=(x_{2}-x_{1},y_{2}-y_{1},z_{2}-z_{1}),\overset{\rightarrow }{AC}=(x_{3}-x_{1},y_{3}-y_{1},z_{3}-z_{1})组成平面基底.
设平面内任意一点P(x,y,z),存在实数\lambda ,\mu 使向量\overset{\rightarrow }{AP}=\lambda \cdot \overset{\rightarrow }{AB}+\mu \cdot \overset{\rightarrow }{AC},
转化为坐标形式有\left\{\begin{array}{l} x=\lambda x_{2}+\mu x_{3}+(1-\lambda -\mu )x_{1}\\ y=\lambda y_{2}+\mu y_{3}+(1-\lambda -\mu )y_{1}\\ z=\lambda z_{2}+\mu z_{3}+(1-\lambda -\mu )z_{1} \end{array}\right.
先挂着吧,慢慢研究,还是希望能够服务于高中生解题.
Ⅱ.平面的法向量与平面的点法式
平面的垂线被称作平面的法线(Normal line),法的意思是,直线的方向规定了平面延展的方向.在计算机图形学中经常和这玩意打交道.

设平面\alpha 的法向量为\overset{\rightarrow }{n}=(a,b,c),平面内一定点A(x_{0},y_{0},z_{0}),
则对于平面内任意一点P(x,y,z),\overset{\rightarrow }{PA}\cdot \overset{\rightarrow }{n}=0(线面垂直的定义),
故点P坐标满足a(x-x_{0})+b(y-y_{0})+c(z-z_{0})=0,即平面的点法式方程.
将其展开得到ax+by+cz+d=0,其中d=-(ax_{0}+by_{0}+cz_{0}),即平面方程的一般式,其为含有三个变量的一次多项式,且多项式系数为法向量的三维坐标,例如:\overset{\rightarrow }{v}=(1,2,3)为平面x+2y+3z+4=0的法向量.
显然这可以帮高中生求平面的法向量,例如:
已知平面过点A(0,0,0),B(1,0,1),C(0,1,1),求平面ABC的法向量.
解:
设平面ABC方程为ax+by+cz+d=0,
\left\{\begin{array}{l} d=0\\ a+c+d=0\\ b+c+d=0 \end{array}\right.,解得\overset{\rightarrow }{n}=(1,1,-1),当然这只是其中一个解.
换一个随意点的例子:
已知平面过点A(1,2,3),B(2,3,4),C(2,1,1),求平面ABC的法向量.
解:
设平面ABC方程为ax+by+cz+d=0,
\left\{\begin{array}{l} a+2b+3c+d=0\\ 2a+3b+4c+d=0\\ 2a+b+c+d=0 \end{array}\right.,即\left\{\begin{array}{l} a+b+c=0\\ 2b+3c=0 \end{array}\right.,解得\left\{\begin{array}{l} a=1\\ b=-3\\ c=2\\ d=-1 \end{array}\right.,
平面方程为x-3y+2z=1,其法向量为\overset{\rightarrow }{n}=(1,-3,2).
①.显然这和数量积等于0那套搞法就是一回事;
②.有没有根据两点坐标求直线方程的感觉;
③.我应该好好学一下线性代数,还有语文.
Ⅲ.截距式
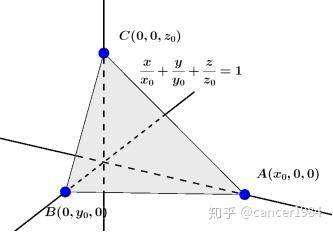
考虑一个特殊的平面,过点A(x_{0},0,0),B(0,y_{0},0),C(0,0,z_{0}),
设平面ABC方程为ax+by+cz+d=0,
\left\{\begin{array}{l} x_{0}a+d=0\\ y_{0}b+d=0\\ z_{0}c+d=0 \end{array}\right.,不妨设d=-1,得\frac{x}{x_{0}}+\frac{y}{y_{0}}+\frac{z}{z_{0}}=1,其法向量为\overset{\rightarrow }{n}=(\frac{1}{x_{0}},\frac{1}{y_{0}},\frac{1}{z_{0}}).
像不像平面中直线的截距式?没别的意思,就是个小福利.
Ⅳ.点到平面的距离
平面外一点为P(x_{0},y_{0},z_{0}),平面方程为ax+by+cz+d=0,求点到平面的距离.
解:
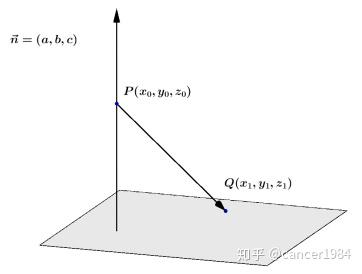
取平面上一点Q(x_{1},y_{1},z_{1}),点到平面的距离为\overset{\rightarrow }{PQ}在法向量\overset{\rightarrow }{n}=(a,b,c)上的投影的绝对值.
根据数量积定义\overset{\rightarrow }{PQ}\cdot \overset{\rightarrow }{n}=| \overset{\rightarrow }{PQ}| \cdot | \overset{\rightarrow }{n}| \cdot \cos \theta ,
故
d=\left| \left| \overset{\rightarrow }{PQ}\right| \cdot \cos \theta \right| =\frac{\left| \overset{\rightarrow }{PQ}\cdot \overset{\rightarrow }{n}\right| }{\left| \overset{\rightarrow }{n}\right| }=\frac{\left| a(x_{1}-x_{0})+b(y_{1}-y_{0})+c(z_{1}-z_{0})\right| }{\sqrt{a^{2}+b^{2}+c^{2}}} \\
点Q(x_{1},y_{1},z_{1})在平面ax+by+cz+d=0上,有ax_{1}+by_{1}+cz_{1}+d=0,带入上式得
d=\frac{\left| ax_{0}+by_{0}+cz_{0}+d\right| }{\sqrt{a^{2}+b^{2}+c^{2}}}.
是不是和他二维兄弟一个模子刻出来的.
二维空间中的直线,三维空间中的平面,两者与所在空间的关系是相同的. |
|