|
|
一、教材及例题说明

本文例题来源于清华大学出版的运筹学(第三版)P79例题1,课本已经讲解了表上作业法的求解过程,本文主要讲解如何用程序求解问题。(在实际解决问题的时候如果采用表上作业法,黄花菜都凉透了。。。)
题目如下所示:

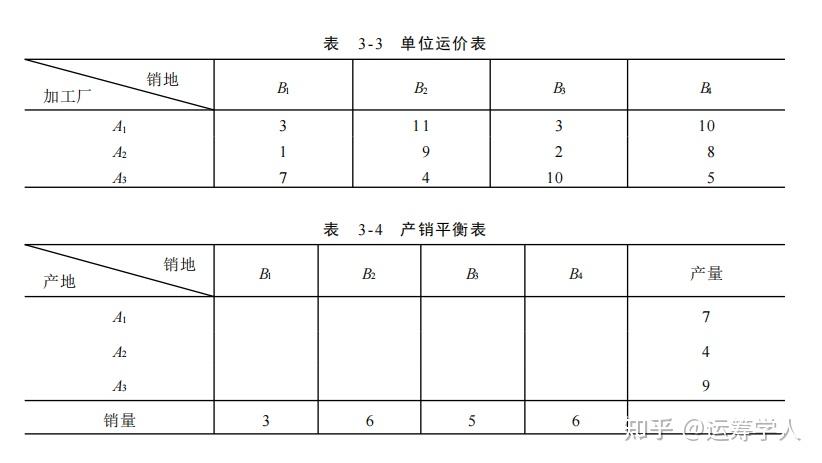
构建如下模型:
min z =\sum_{i=1}^{3}\sum_{j=1}^{4}{c_{ij}}{x_{ij}}
\sum_{i=1}^{3}{x_{ij}}=b_{j},j=1,2,3,4
\sum_{j=1}^{4}{x_{ij}}=a_{i},i=1,2,3
\sum_{i=1}^{3}\sum_{j=1}^{4}{x_{ij}}\geq0
根据运价表和产销平衡表构建如下数学模型:
min z =3*x_{11}+11*x_{12}+3*x_{13}+10*x_{14}+1*x_{21}+9*x_{22}+2*x_{23}+8*x_{24}+7*x_{31}+4*x_{32}+10*x_{33}+5*x_{34}
x_{11}+x_{12}+x_{13}+x_{14}=7 (1)
x_{21}+x_{22}+x_{23}+x_{24}=4 (2)
x_{31}+x_{32}+x_{33}+x_{34}=9 (3)
x_{11}+x_{21}+x_{31}=3 (4)
x_{12}+x_{22}+x_{32}=6 (5)
x_{13}+x_{23}+x_{33}=5 (6)
x_{14}+x_{24}+x_{34}=6 (7)
二、采用面向过程思维求解
这也是一个线性规划问题,可以按照我们前一节中讲的五步法求解,先展示以下过程,然后再说这种方法的弊端。具体代码如下:
package cplex.practice;
import ilog.concert.*;
import ilog.cplex.*;
public class TransportionProblem {
public static void main(String[] args) {
try {
// 1、定义模型
IloCplex cplex = new IloCplex();
// 2、定义参数变量
double[] lb = new double[12];
for(int i=0; i<lb.length; i++) {lb=0;}
double[] up = new double[12];
for(int i=0; i<up.length; i++) {up=Double.MAX_VALUE;}
IloNumVar[] x =cplex.numVarArray(12, lb, up);
// 3、定义目标函数
// 定义目标函数系数
double[] objvals = {3, 11, 3, 10, 1, 9, 2, 8, 7, 4, 10, 5};
//定义目标函数
cplex.addMinimize(cplex.scalProd(x, objvals));
// 4、定义约束条件
IloNumExpr cs1 = cplex.numExpr();
IloNumExpr cs2 = cplex.numExpr();
IloNumExpr cs3 = cplex.numExpr();
for(int i=0;i<3;i++) {
for(int j=0; j<4; j++){
switch(i){
case 0:
cs1= cplex.sum(cs1,x[i*j+j]);
continue;
case 1:
cs2= cplex.sum(cs2,x[i*4+j]);
continue;
case 2:
cs3= cplex.sum(cs3,x[i*4+j]);
continue;
}
}
}
cplex.addEq(cs1,7);
cplex.addEq(cs2,4);
cplex.addEq(cs3,9);
IloNumExpr cs4 = cplex.numExpr();
IloNumExpr cs5 = cplex.numExpr();
IloNumExpr cs6 = cplex.numExpr();
IloNumExpr cs7 = cplex.numExpr();
for(int j=0;j<4;j++) {
for(int i=0; i<3; i++){
switch(j){
case 0:
cs4= cplex.sum(cs4,x[i*4+j]);
continue;
case 1:
cs5= cplex.sum(cs5,x[i*4+j]);
continue;
case 2:
cs6= cplex.sum(cs6,x[i*4+j]);
continue;
case 3:
cs7= cplex.sum(cs7,x[i*4+j]);
continue;
}
}
}
cplex.addEq(cs4,3);
cplex.addEq(cs5,6);
cplex.addEq(cs6,5);
cplex.addEq(cs7,6);
// 5、求解、获得并展示结果
if(cplex.solve()) {
cplex.output().println(&#34;Solution status = &#34; + cplex.getStatus());
cplex.output().println(&#34;Solution value = &#34; + cplex.getObjValue());
double[] val = cplex.getValues(x);
// for (int j = 0; j < val.length; j++) {
// cplex.output().println(&#34;x&#34; + (j+1) + &#34; = &#34; + val[j]);
// }
for (int i = 0; i < 3; i++) {
for(int j = 0; j<4; j++) {
cplex.output().print(&#34;x&#34; + (i*4+j) + &#34; = &#34; + val[i*4+j]+&#34; &#34;);
}
System.out.println();
}
}
else {System.out.println(&#34;No feasible solution!&#34;);}
}
catch(IloException e) {
System.err.println(&#34;Concert exception caught:&#34; + e);
}
}
}
三、结果展示
程序求解结果:
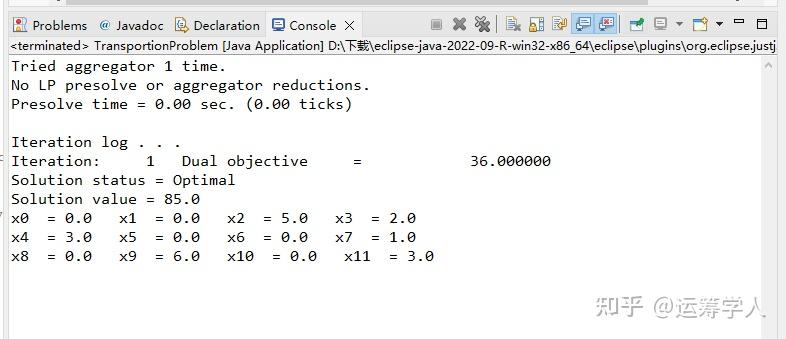
教材求解结果:
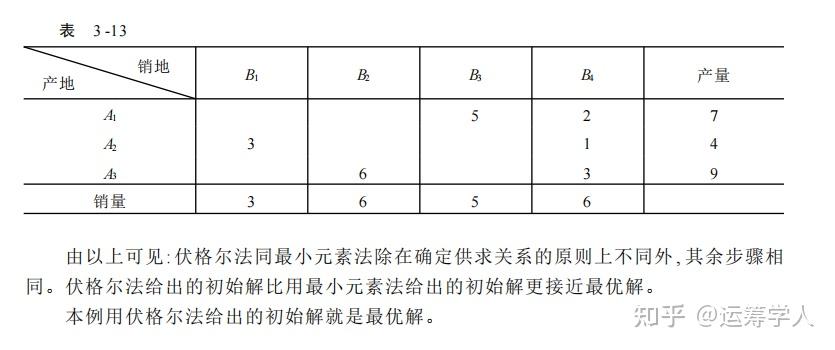
两者是一致的。
四、面向过程求解方法优、缺点分析
优点:代码过程直观、好理解;
缺点:代码通用性差,如果运输节点、需求、运价等数据发生变化,改动代码比较麻烦,容易出错。
下一节将介绍如何利用面向对象思维求解运输问题。
PS : 文章中有任何问题,欢迎大家批评指正! |
|