|
|
关于3D平面的一些小知识总结,主要是一些中学数学知识。
3D平面的定义方式有多种,不过所有的方式都可以由最简单的形式(即不在同一直线上的三个点确定一个平面)推导出。
1 一般式
假设我们有三个点 p_0, p_1, p_2 ,如图1所示。
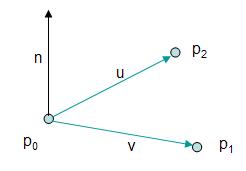
图1 确定一个平面的三个点及其法线
本文主要参考这篇文章,图1也来自它。 图1中三个点对应的平面的平面方程(即空间中所有处于同一平面的点所对应的方程)最常见的形式:
Ax+By+Cz+D=0
系数 A, B, C, D 计算方法如下:
- 计算向量 v=p_1 - p_0 ,向量 u=p_2 - p_0
- 计算 n=v\times u (叉乘)
- 归一化(normalize) n
- 实际上上面得到的 n 即为平面法线,则
5. 为了计算 D ,只需要代入平面内的任意一点,比如, p_0 ,得到 D=-(Ax+By+Cz)=-n\cdot p_0 (点乘)
为什么平面方程是这样的?其实给定平面上的一个点p和平面的法线n,就可以确定该平面了。因为对于平面上任意一点q=(x, y),向量pq一定垂直于法线n。而点p与平面外的点的连线对应的向量和n是不垂直的。而垂直的定义就是点积为0,即 n\cdot(q-p)=0 ,即 n_x(x-p_x) + n_y(y-p_y)+n_z(z-P_z)=0 ,即 n_x x+n_y y + n_z z - (n_x p_x + n_yp_y+n_zp_z)=0 ,这恰好就是最上面的平面方程的常见形式。这种由一个点及法线表示平面方程的方法叫点法式。 2 截距式
当平面方程的一般式 Ax+By+Cz+D=0 ,中 D\neq 0 时,设 a=\frac{-D}{A}, b=\frac{-D}{B}, c=\frac{-D}{C} ,可推导出平面方程的截距式: \frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1 。
则此截距式平面方程对应的平面与三个坐标轴的交点分别为 (a, 0, 0), (0, b, 0), (0, 0, c) ,其中 a, b, c 依次为该平面在x, y, z轴上的截距。
3 点到平面的距离
假设已求得了平面的一般式方程 Ax+By+Cz+D=0 ,另设三维空间中有一点 r=(x_r, y_r,z_r) ,则 r 到此平面的距离为:
dist=Ax_r + By_r + C*z_r+D=n\cdot r + D
实际上点 r 到平面的距离应该是此处 dist 的绝对值。也即此处的 dist 是一个有符号距离,如果 dist 为0,则表面点r在平面上; 如果 dist 大于0, 则r在法线n所指的那一边;如果 dist 小于0,则r在法线所指的反方向那一边。即有符号距离 dist 是很有用的,通过它就可以判断点在平面的哪一边。
为啥点到平面的距离是这样计算的?很简单,此处略微说明:
要求点 r 到平面的距离,只需要找平面上任意一点 p_0 ,求从 p_0 指向 r 的向量 v ,把 v 投影往平面的单位法线 n 上做投影(即 v\cdot n ),则投影的长度即为点 r 到平面的距离。此处主要用到向量点积,以及一个潜在条件: Ax_0+By_0+Cz_0+D=0 。很容易证明。
由此可知,原点(0, 0, 0)到平面的距离恰好就是D 4 把点投影到平面
注意 1中已说明(A, B, C)是平面的单位法向量,则 A^2+B^2+C^2=1 。
设三维空间中一点p=(x, y, z),要求p在平面上的投影点q。
易知pq垂直于平面,则pq平行于平面的法线(A, B, C)。所以,设参数t,则:
\frac{x - x_q}{A}=\frac{y-y_q}{B}=\frac{z-z_q}{C}=t,
所以:
x_q = x - tA, \quad y_q=y-tB,\quad z_q = z-tC
又投影点q在平面上,所以满足平面方程:
Ax_q + By_q + Cz_q + D = 0,
即:
A(x-tA)+B(y-tB)+C(z-tC)+D=0
可求得:
t=\frac{Ax+By+Cz+D}{A^2+B^2+C^2}=Ax+By+Cz+D=dist
其中 dist 即为点p到平面的垂直有向距离
故,投影点为 q=p-n*dist
References:
|
|